
 |
|
Главная Длительная эволюция [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [ 14 ] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] X /. sols г -l~Sqrt[b] -1 + Sqrt[bh 1 2 2 / У рассмотренного уравнения достаточно простые корни, поэтому обратимся к новому примеру; 2.5. Алгебраические и трансцендентные уравнения Уравнения и методы получения их решений - один из важнейших разделов математики. Ниже мы рассмотрим основные функции, применяемые для нахождения символьных решений алгебраических и трансцендентных уравнений. Начнем со случая одного уравнения относительно одной неизвестной: sols = Solve[x3 - 2х + 1 == 0,х] Уравнение е = -2х + 1 == О, записанное с помощью предиката Equal, является первым аргументом функции Solve - основной функции, применяемой для решения уравнений. Второй аргумент - переменная, относительно которой решается уравнение. Результатом вычисления выражения с заголовком Solve является список, элементами которого являются одноэлементные списки. Эти элементы есть подстановки вида х ехрг{. Выражение ехрг, - это то, что обычно понимается под корнем уравнения. Если в уравнении е сделать подстановки, полученные в результате вычислений, то результатами будут True, если корни найдены правильно: хЗ - 2х -Ь1 /. sols {True, True, True] Чтобы получить список корней, достаточно сделать подстановку: newsols = Solve[x"3 - Зх +1 == 0,х] 3 2? . (-27 + 27;5grt[3]) (-27-f-27/5gri[3]) 3 2з -3{1+ ISqrt[3]) 2f(-27 + 27/5gr«[3])3 (1 - /5г[3])(-27 + 27/5grf[3])з -3(1 - ISqrt[3]) 23 (-27 -f 27/59ri[3])J (l + /5grt[3])(-27 + 27/Sgr[3])3 625 В полученных формулах / - встроенная константа, мнимая единица г. На первый взгляд, все три корня - комплексные числа с не равными нулю мнимыми частями. На самом деле корни вещественные. Чтобы в этом убедиться, воспользуемся функцией N, дающей приближенное численное значение выражений, и функцией Plot, рисующей графики. Вычислим выражение: N [newsols] {{х 1.53209 - 3.33067 10"/}, {х -1.87939 - 3.88578 10-/}, {х0.347296 + 9.99201 Ю!}} Результат показывает, что мнимые части корней имеют одинаковый порядок 10. Попробуем увеличить точность вычислений. Для этого воспользуемся тем, что второй необязательный аргумент у функции N задает число значащих цифр вещественных чисел. N[newsols,25] {{х 1.532088886237956070404785-f-O.lO"/} {х -1.879385241571816768108219 + 0.10"/}, {х -> 0.347296355333860697703433 - O.IQ-/}} Теперь порядок мнимых частей корней Ю". Это говорит о том, что корни - вещественные. Наглядное представление о расположении корней можно получить, нарисовав график функции х - Zx + l с помощью функции Plot (рис. 2.1): Plot[x-3 - Зх +1, {х, -2,2}] 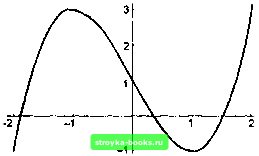 Рис. 2.1 График наглядно показывает, что кубическая парабола - Зх -f 1 пересекает ось абсцисс в трех точках. Присутствие в newsols мнимой единицы есть результат следующего выбора ветви многозначной функции 2(1/*=) комплексного аргумента Z. Аргумент ip любого комплексного числа считается изменяющимся от -тг до тг, поэтому г/* имеет аргумент (р/к. Например, (-1)/ т.е. кубический корень из минус единицы, равен 1/2 + /\/5/2. Иное по сравнению с Solve представление для корней уравнений дает функция Roots. rts = Roots [е,х] -l~Sqrt[5] x = l -l-{-Sqrt[5] [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [ 14 ] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.001 |