
 |
|
Главная Длительная эволюция [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [ 29 ] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] FilledPlot очень полезна для решения уравнений и неравенств (рис. 3.14): FilledPlot[{Sin[x], O.lx}, {х, 0,4Pi}, Fills -+{{1,2}, GrayLevel[0.9]}]; 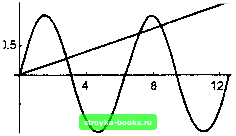 -0.5 Рис. 3.14 На экране дисплея закрашена серым цветом область, заключенная между графиками функций Sin[x] и O.lx. В общем случае графиков может быть несколько, закрашиваться своим особым цветом могут области, заключенные между любыми парами графиков, а также между каким-то графиком и осью Ох. Функция FilledPlot имеет дискретный аналог ListFilledPlot (рис. 3.15): List FilledPlot [{2,3,2,2,5,3}]; 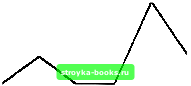 Часто кривые на плоскости задаются в полярных координатах. Если воспользоваться функцией PolarPlot, то их не нужно пересчитывать в декартовы координаты для функции Plot. Гистограммы для дискретных данных получаются с помощью нескольких функций, являющихся модификациями функции BarChart. Пусть даны два массива данных datal = = {2,3,2,2,5,3} и data2 = {3,2,1,5,6,3}, тогда их гистограмма (рис. 3.16) может быть получена вычислением выражения BarChart[datal, data2] 2 3 4 Рис. 3.16 Функция PieChart рисует круговые гистограммы данных (рис. 3.17): PieChart[datal] 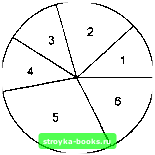 / = Line[{{0,0},{l/2,2},{3/2,2},{2,0}}] Превратить их в рисунок на экране дисплея можно следующим способом. Сначала к ним нужно примейить функцию Graphics, трансформируя их в один из шести графических объектов ( Graphics, DensityGraphics, ContourGraphics, Graphics3D, Sur-faceGraphics и GraphicsArray), a к результату применить функцию Show (рис. 3.18): Show[Graphics[{p, 1}]]; 3.7. Графические примитивы Двух- и трехмерные рисунки, которые выполняются графическими функциями, состоят из графических примитивов, таких, как точки, линии, многоугольники, круги, диски, параллелепипеды, текст. Точка двумерного рисунка как графический примитив есть выражение вида Point[{x,y}], где X и у суть декартовы координаты точки на плоскости. Линия есть на самом деле ломаная линия, состоящая из отрезков прямых, соединяющих последовательные угловые точки этой линии: Line[{{xi,yi},{x2,y2},•••}]• Рассмотрим два графических примитива: p = Point[{l,l}] [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [ 29 ] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.001 |