
 |
|
Главная Длительная эволюция [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [ 30 ] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] Кроме графических примитивов имеются графические директивы, определяющие размеры, цвет и стиль представления примитивов на экране. Если они не указаны явно, как в только что рассмотренном примере, то они устанавливаются по умолчанию. Директивы PointSize[r] и AbsolutePointSize[r] определяют относительный и абсолютный размеры точки как круга радиуса г. В первом случае г есть отношение радиуса к ширине полного рисунка, во втором случае - г есть радиус в единице длины, приблизительно равной одной семьдесят второй дюйма. Директива ставится перед примитивом, и оба эти объекта заключаются в фигурные скобки. Кроме того, директива может действовать на несколько однородных примитивов, стоящих за ней. Вся группа также заключается в фигурные скобки. Графических директив может быть несколько, и они должны предшествовать, примитивам. Вычисление выражения S how [G rap hies [{Point size[0.03], Н ue[0], Table[Point[{0.1j,0.05j}],{j,5}]}]]; приводит к появлению на экране пяти точек красного цвета относительного размеры 0.03. Директивами, управляющими представлением линии, кроме цвета, являются Thickness[r] и AbsoluteThickness[r]. Они определяют относительную и абсолютную ширину линии. Директива Dashing[{rl,r2,...}] имеет результатом представление линии в виде совокупности отрезков длины г1, г2 и т.д., которые повторяются циклически. Пусть / есть следующий примитив: / = Line[{{0,0},{l,l},{0.95,0.98}, {1,1}, {0.98,0.95}}] тогда можно получить следующий рисунок (рис. 3.19):  Рис. 3.20 На цветном мониторе получается заполненный красной краской равносторонний треугольник. Частный случай многоугольника - прямоугольник - можно получить с помощью примитива Rectangle [{{xmin, у min}, {xmax,ymax}], в котором [xminyrain) - координаты нижнего, а [хтахутах] - координаты верхнего углов прямоугольника. Дугу окружности рисуют, прибегая к графическому примитиву Circle[{x,y}, г>{1,2}] и указывая координаты (а:,у) центра окружности, Show[Graphics[{Dashing[{0.05,0.03}], Thicknessjo.Ol],!}]]; Рис. 3.19 Графический примитив Polygon[{xl,yl}, {х2,у2}, ...}] представляет заполненный многоугольник, ограниченный замкнутой ломаной линий, проходящей через точки (а;1,у1), (а;2,у2) и т.д. (рис. 3.20): Show[Graphics[{Hue[0], Polygon[{{0,0}, {1,1}, {2,0}}]}]]; радиус г и граничные значения (1,2) полярного угла. Закрашенный круг получается с помощью примитива Disk[{x,y},r]. Важным графическим примитивом является тот, который задает текст: Text[expr, {х,у}]. В этом выражении ехрг есть любое выражение, и печатная форма вычисленного выражения будет центрирована относительно точки с координатами х,у. Если сначала нарисовать график параболы у= {2 + х) на отрезке [-3,-1] и обозначить через р графический объект р = Plot[(2 -- х)"2, {х, -3, -1}], то этот рисунок можно снабдить текстом (рис. 3.21): Show[p,Graphics[{Text["Graph of y="Expand[(2--x)-2], {-2,0.9}]}]]; Graph of у = 4 + 4x + 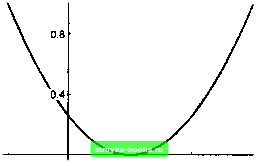 -1.5 Рис. 3.21 Внести текст или другие графические примитивы в рисунки, созданные встроенными графическими функциями, можно с помощью опций Prolog и Epilog. По умолчанию они установлены на пустой список {}. Пользователь может внести в этот список любые подходящие случаю примитивы. Разница между рассматриваемыми опциями состоит в том, что примитивы опции Prolog рисуются до, а примитивы опции Epilog - после основного рисунка (рис. 3.22): [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [ 30 ] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.001 |