Plot [{ Airy AiPrime[x], Airy Ai[x]}, {x, - 5,5}, Prolog {Text[FontForm[" AiryAiPrime", {"Times", 14}], {1.4,-О.З}],

Text[FontForm[" AiryAi", {"Eurostyle",14}], {1,0.4}]} PlotLabel FontForm["TwoGraphs", {"Courier", 14}], PlotStyle -> {{Dashing[0.02]},{GrayLevel[0.8]}}]

Two Graphs

Рис. 3.22

В графическом примитиве Text была использована функция FontForm, аргументами которой являются строка с текстом, название и размер шрифта.

Если вместо заголовка Graphics воспользоваться заголовком Graphics3D, то можно получать трехмерные рисунки. При этом примитивы Point, Line, Text и Polygon с соответствующими изменениями переносятся на трехмерный случай. Единственным новым трехмерным примитивом является

Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}],

с помощью которого рисуется параллелепипед с противоположными углами в точках с координатами хтгп, ymin, zmin и хтах, утах, zmax (рис. 3.23):

Show[Graphics3D[{GrayLevel[0.8],Cuboid[{0,0,0}, {1,1,1}]}],

Boxed False, Lighting -> False];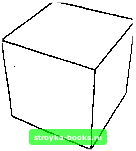

Рис. 3.23

Как и в двухмерном случае, рисунки, отвечающие разным примитивам, можно накладывать друг на друга (рис. 3.24):

S how[Graphics3D [{GrayLevel[0.9], Cuboid[{0,0,0}, {1,1.1}]}],

Graphics3D[{Hue[0],Thickness[0.01], Line[{{-l,0,0},{2,l,l}}]}], Graphics3D[{Hue[0.6],PointSize[0.04], Point[{-l,0,0}]}],],

Graphics3D[{Hue[0.6],PointSize[0.04],Point[{2,l,l}]}], Boxed -> False, Lighting -> False];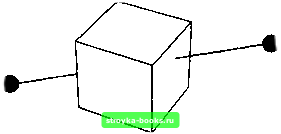

Упражнения

1. Касательная как предельное положение секущих. Постройте совместные графики функции /(i) = sini, касательной к графику этой функции в точке 0.5 и пяти секущих, проходящих через точку (0.5,/(0.5)) и точки (0.5 - j 0.04,/(0.5 -i 0.04)), j - 5,4,3,2,1, на интервале от 0.01 до 1. Окрасьте график функции /(х) в синий, касательную в красный и секущие в зеленый цвета. Подберите толщину кривых так, чтобы рисунок был наиболее выразителен. Сделайте мультфильм из серии рисунков, на каждом из которых нарисованы графики функции, касательной и одной из секущих.

2. Постройте совместные графики функции f{x) = 5х* - 12х + 8х + 2 и ее производной на интервале (-1,2). Окрасьте график функции в синий, а ее производной в красный цвета. Сравните интервалы убывания и возрастания функции со знаком ее производной.

3. Какой функцией из директории Graphics следует воспользоваться, чтобы нарисовать лемнискату 4(i + У) = 41(i - у)? Какие опции следует установить с тем, чтобы лемниската имела фиолетовый цвет и относительную толщину 0.01?

4. В рисунке Two Graphics отметьте графики функций AiryAiPrime(x) и AiryAi(x) вместо надписей маленькими квадратом и треугольником.

5. Формулы I = ch(u)cos(t), у = sh(u)sin(t) задают переход к эллиптической системе координат. Линии постоянного и суть эллипсы, линии постоянного t суть гиперболы. Постройте рисунок, содержащий пять линий постоянных и и пять линий постоянных t. Используйте для этого функции ParametricPlot, Table, Show.

6. Подгрузите пакет GraphicsShapes, сделав доступными следующие геометрические объекты: Cylinder (цилиндр). Cone (конус), Torus (тор), Sphere (сфера), MoebiusStrip (лист Мебиуса), Helix (спираль) и DoubleHelix (двойная спираль). Что нужно сделать, чтобы нарисовать эти объекты?

7i Подгрузите пакет GraphicsPolyhedra и узнайте названия многогранников, которые можно нарисовать с помощью функций этого пакета. Задав вопрос ?Cube, узнаете, что нужно сделать, чтобы нарисовать их с помощью функции Show. Нарисуйте эти объекты.