
 |
|
Главная Длительная эволюция [0] [1] [2] [3] [4] [5] [ 6 ] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] Попробуем теперь найти корни уравнения + 2х - 1 = 0. rts = Solve[x"5 + 2х - 1 == 0,х] {ToRules[Roots[2x + х==1, х]]} Подобный ответ означает, что формул для корней рассматриваемого уравнения не существует. Тем не менее можно узнать численное значение всех пяти корней, вычислив выражение N[rts]. N[rts] { {х -0.945068 - 0.854518 /}, {i -0.945068 + 0.854518 /}, {х 0.486389}, {х 0.701874 - 0.879697/}, {х 0.701874 + 0.879697 /} } Можно убедиться в правильности вычисления хотя бы одного вещественного корня, нарисовав график многочлена х+ --2х - 1 с помощью графической функции Plot (рис. 1.1): Plot[x"5 -Ь 2х - 1, {х, -1,1}] 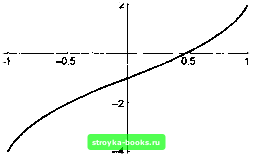 - Graphics - Рис. 1.1 Действительно, график рассматриваемого многочлена пересекает ось Ох вблизи от точки X = 0.5. Сообщение - Graphics -означает, что „Математика" сформировала описание представленного графика на языке PostScript. Вот фрагмент этого описания: %% Creator: Mathematica %%AspectRatio: .6103 MathPicture Start %%Graphics / Courier findfont 10 scalefont setfont %Scaling calculations 0.5 0.47619 0.407118 0.0981006 [ [(-1)] .02381 .40712 0 2 Msboxa Рассматриваемый текст можно увидеть и при необходимости отредактировать, расформатировав ячейку, в которой содержится график. Для этого ячейку выделяют и выполняют Cell Formatted. Этот и ему подобные тексты можно преобразовать в различные графические форматы: EPS, PICT, PCX и другие, сохранить в файле, использовать для вставки в текст статьи, чтобы послать коллегам по электронной почте и т.п. Возвращаясь к решению уравнений, заметим, что „Математика" умеет численно решать не только полиномиальные, но и трансцендентные уравнения. Правда, если заранее известно, что какое-то уравнение имеет бесконечно много корней, следует указать хотя бы грубое приближение к искомому корню. Последнее можно найти, нарисовав график соответствующей функции. Предположим, что нам нужно найти первый после нуля корень функции Бесселя первого порядка Ji аргумента -/х, т.е. корень функции Ji{y/x) (рис. 1.2). Plot[BesselJ[l,Sqrt[x]],{x,l,20}] 0.6 г 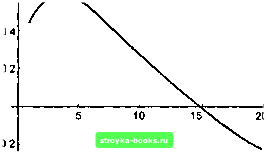 - Graphics - Рис, 1.2 Мы видим, что в рассматриваемом интервале корень уравнения существует и лежит вблизи точки х = 15. Уточним его значение. FindRoot[BesselJ [1, Sqrt[x]], {х, 15} ] {х -> 14.682} МАТЕМАТИЧЕСКИЙ АНАЛИЗ. Наряду с алгебраическими преобразованиями „Математика" позволяет выполнять операции математического анализа. Естественно, что базовыми являются операции интегрирования Integrate и дифференцирования D (вновь исключение, впрочем, последнее из правила): int = Integrate[x5/Sqrt[x3 - 1],х] Проверим правильность полученного ответа дифференцированием: [0] [1] [2] [3] [4] [5] [ 6 ] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.0012 |