
 |
|
Главная Длительная эволюция [0] [1] [2] [3] [4] [5] [6] [ 7 ] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] difint Simplify Sqrt[-l + x] Одной из важнейших математических задач является нахождение решений обыкновенных дифференциальных уравнений. Для этой цели предназначена функция DSolve, первым аргументом которой является дифференциальное уравнение или система дифференциальных уравнений. Если у[х] есть неизвестная функция, то производная от нее может быть записана во входном формате как у[х]. Вторым аргументом функции DSolve является неизвестная функция, а третьим - независимая переменная. DSolve[x~2 у"[х] + х у[х] + х"2 у[х] == 0,у[х],х] { {у(х) BesselY[О, х]С[1] + BesselJ[Q, х] С[2]} } Получено общее решение исследуемого дифференциального уравнения, являющееся линейной комбинацией с коэффициентами С[1] и С[2] функций Бесселя нулевого порядка первого и второго рода. , Функцию DSolve можно применять и для решения систем обыкновенных дифференциальных уравнений. difint = D[int,x] 2Sqrt[-l + x] 3 Полученный результат не совпадает с исходным выражением. Попробуем его упростить: DSolve[{y[x] == a-2z[x] - Sin[x],z[x] == y[x] + b} {y[x],z[x]},x], He все обыкновенные дифференциальные уравнения и системы уравнений допускают явные точные решения, поэтому приходится прибегать к численным методам. Обратимся к системе обыкновенных дифференциальных уравнений, описывающих плоское движение двух гравитирующих тел. Пусть масса второго тела в 1,3 раза больше массы первого. В этом случае движение описывается следующей системой обыкновенных дифференциальных уравнений: masses = {xl"[t] == -1.3(xl[t] - x2[t]) / ((xl[t] -x2[t])-2+ (yl[t] -y2[t])2)-(3/2), yl"[t]==-1.3(yl[t]-y2[t])/ ((xl[t]-x2[t])2 + (yl[t]-y2[t])-2)-(3/2), x2"[t] ==-(x2[t]-xl[t])/ ((xl[t] - x2[t])-2+ (yl[t] -y2[t])-2)-(3/2), y2"[t] ==-(y2[t]-yl[t])/ ((xl[t] -x2[t])-2+ (yl[t] -y2[t])-2)-(3/2)}; Знак пунктуации ; (точка с запятой), поставленный в конце входного выражения, блокирует вывод на экран результата вычисления, хотя рассматриваемая система присвоена в качестве значения символу masses. Снабдим систему masses следующими начальными данными: init - {х1[0] == 1,х1[0] == 0,у1[0] == 0,у1[0] == 0.3, х2[0] == -10/13,х2[0] == 0,у2[0] == 0,у2[0] == -3/13}; И найдем численное решение поставленной задачи Коши на интервале 0<t <4. Для численного решения задач Коши для систем обыкновенных дифференциальных уравнений предназначена функция NDSolve. Ее первый аргумент - исследуемая система, дополненная начальными условиями; второй аргумент - список имен неизвестных функций; третий аргумент - список, содержащий независимую переменную, начальную и конечную точки интервала численного интегрирования системы. п = NDSolve[ Join[masses, init] ,{xl,yl,x2,y2},{t,0,4}] { {il InterpolatingFunction[{0.,A.},< >], yl InterpolatingFunction[{0.,4.}, < >], x2 InterpolatingFunction[{0.,4.}, < >], у2 - InterpolatingFunction[{0.,4.},<>],}} Результатом вычисления являются четыре интерполяционные функции, используя которые можно нарисовать орбиты тел (рис. 1.3): ParametricPlot[{Evaluate[{xl[t],yl[t]},/.n], Evaluate[{x2[t],y2[t]}/.n]},{t,0,4}, AspectRatio -> Automatic]; 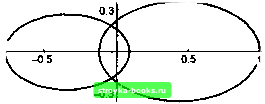 Рис. 1.3 Начальные данные подобраны так, что гравитирующие тела описывают замкнутые эллиптические орбиты. Поскольку вычисления занимают мало времени, читатель может начать [0] [1] [2] [3] [4] [5] [6] [ 7 ] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.0009 |