
 |
|
Главная Длительная эволюция [0] [1] [2] [3] [4] [5] [6] [7] [ 8 ] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] изучение закономерностей движения тел, изменяя числовые параметры в init или masses. „Математику" можно использовать как справочник специальных математических функций: Бесселя, Лежандра, Эйлера, Эйри, Эрмита и т.д. Сведения об асимптотических разложениях функции Бесселя первого рода второго порядка в окрестностях точек О и оо можно получить, используя функцию Series, следующим образом: { Series [BesselJ [2, х], {х, 0,2}], Series[BesselJ[2, х], {х. Infinity, 2}]} Sqrt[2]Sqrt[]{Cos[- - - + 0[i]3) В полученной формуле символ Pi есть число тт. С помощью функции Series можно раскладывать в асимптотические ряды произвольные функции: Series[(f [х + h] - 2f [х] -- f [х - h]) /h-2, {h,0,3}] АППРОКСИМАЦИЯ. Рассмотрим задачу о наилучшем среднеквадратичном приближении. Предположим, что в файле file.val, расположенном в вашей рабочей директории, хранятся экспериментальные данные. Содержимое файла можно увидеть, выполнив команду: !!file.val 1 -0.75 0.2 0.81077 0.4 1.31766 И т.д. (мы не приводим всех строк файла в целях экономии места). В файле содержатся пары вещественных чисел, записанные построчно и представляющие значения абсцисс и ординат экспериментальных данных. Файл можно ввести в Записную книжку с помощью команды ReadList, присвоив символу data значение соответствующего списка: data = ReadList["file.val",{Number,Number}] {{О, -0.75}, {0.2,0.81077}, {0.4,1.31766}, {0.61,1.63181}, {0.8,2.2533}, {1., 1.75}, {1.2,1.23509}, {1.4,1.45863}, {1.6,1.293237}, {1.8,0.914413}, {2., 1.245},{2.2,1.82007}, {2.4,1.72712}, {2.6,2.21069}, {2.8,3.719648}, {3., 3.75} } Представим данные data в виде дискретного грги)ика (рис. 1.4): р1 = ListPlot[data,PlotStyle {PointSize[0.01], RGBColor[l,0,0]}]; Рис. 1.4 Попробуем аппроксимировать дискретные данные data на отрезке от О до 3 с помощью полинома четвертой степени: ро1у4 = Fit[data,{l,x,x"2,x"3,xM},x] -0.728077 + 8.773731 - 9.6255x2 + 3.78372а;3 0.459172а;» Нарисуем график этого полинома на отрезке О < х < 3 (рис. 1.5): р2 = Plot[poly4,{x,0,3},PlotStyle- {{Thickness[0.007], RGBColor[l,0,l]}}]; 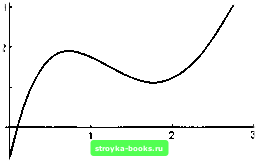 Рис. 1.5 С помощью функции Show совместим два последних графика (рис. 1.6). Если точность приближения неудовлетворительна, можно взять многочлен более высокой степени. Show[pl,p2]; 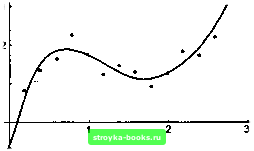 Рис. 1.6 [0] [1] [2] [3] [4] [5] [6] [7] [ 8 ] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.001 |