с краевым условием на границе Г Э7-

Х(х, q. 7-)

- а(х, q, Г)(7-Гс)= О, (2.62)

где X - теплопроводность элементов конструкции; Т - температура в изделии; w - удельная мощность, вьщеляющаяся в изделии; а - коэффициент теплоотдачи во внещнюю среду; - температура окружающей среды.

Уравнения (2.61) и (2.62) являются нелинейными, так как тепло-физические характеристики и условия теплоотдачи зависят не только от вектора пространственньгс координат х, но также и от температуры Т- Рещение их зависит также от вектора конструктивных параметров q размерности М.

В переходном режиме тепловые режимы силовых резисторов опи-сьшаются уравнением

С(х, q, Т) =- V(X (X, q, Г) V 7) + W (х, q, Т, т) (2.63)

с краевым условием (2.62) и начальным условием

(х, q, 0) = Го, (2.64)

здесь г -время; С - теплоемкость элементов конструкции.

В общем случае для расчета тепловых режимов силовых резисторов необходимо решать нелинейные уравнения (2.61) - (2.64). что требует значительньгх затрат машинного времени. Для решения их воспользуемся методом электротепловой аналогии. Разобьем конструкцию на ряд элементов, каждому из элементов поставим в соответствие температуру 7}, тепловую проводимость а,-, теплоемкость Q.

Полученная таким образом система уравнений относительно вектора температур Т эквивалентна разностной аппроксимации уравнений (2.61) и (2.62):

G(T-Tc) = (2.65)

Для г-го элемента имеем Nk

Е а,- (7/ - 7}) = г = 0,1,2,..., N, i ф /, / = 0

где а. - тепловая проводимость между г-м и/-м элементами конструкции силового резистора.

В качестве нулевого элемента принимается окружающая среда. Элементы матрицы Gjy можно записать в виде

"Тдоп"

где е 1.

Обычно для решения системы (2.65) достаточно трех-четырех итераций. Расчет тепловых режимов для силовых резисторов с сильной зависимостью электрической проводимости РЭ от температуры, например для варисторов, требует 7-10 итераций.

На рис. 2.20, а приведена зависимость погрешности решения от числа итераций.

Выбор числа разбиений конструкции силового резистора на элементы определяется, с одной стороны, требуемой точностью, а с другой - ресурсами, необходимыми для подготовки данных и решения системы (2.65). Действительно, объем вычислений зависит от числа элементов конструкции как N, так что при увеличении числа разбиений вдвое объем вычисления возрастает в 8 раз, а объем памяти, необходи-

Следует отметить, что для большинства конструкций матрица G - редкозаполненная, т.е. большинство элементов Gj-y равно нулю. Кроме того, система уравнений (2.65) слабо нелинейна.

Значения тепловых проводимостей элементов конструкции обусловливаются механизмами переноса тепловой энергии. Формулы для расчета, а также справочные данные по теплофизическим характеристикам материалов, применяемых при изготовлении силовых резисторов, приводятся в [11, 16, 30-32]. В пакете прикладных программ TERMO значения тепловых проводимостей рассчитываются автоматически по описанию схемы замещения; формулы для расчета и тепло-физические характеристики являются частью математического обеспечения.

Решение системы нелинейных уравнений (2.65) осуществляется итерационным методом. Вначале тепловые сопротивления в (2.65) рассчитываются для значения температуры в изделии, равном

Т*» =Те+ Тдоп/2.

Далее зависимость тепловых сопротивлений от температуры "замораживается" и решается система линейных уравнений относительно Т. Элементы матрицы С для второй итерации рассчитьшаются для распределения температур Т и т.д. Условием завершения итерационного процесса является

11т-т-Ч1 • .

< е.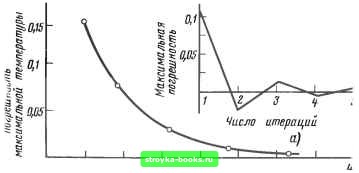

15 ZD 25 3D 35 Число разбиений. б)

Рис. 2-20. Погрешности решения задачи расчета установившегося теплового режима:

а - итерационное уточнение решения; б - зависимость погрешности от числа разбиения конструкции силового резистора

мой для хранения матрицы G, в 4 раза. На рис. 2.20, б представлена зависимость погрешности расчета стационарного теплового режима пепроволочного силового резистора цилиндрической формы от числа разбиений. Следует отметить, что данпьЕ рис. 2.20, б носят ориентировочный характер, вид зависимости погрешности от числа разбиений в значительной степени отличается от конструкции к конструкции.

Рекомендуется следующая методика определения максимальной температуры в изделии. Конструируются три тепловые схемы замещения изделия с числом элементов Nki <-Nk2 Nk3- При уточнении схемы замещения желательно наиболее подробное разбиение конструкции вьшолнять в окрестности элемента с максимальной температурой. Зависимость максимальной температуры Ттах от числа разбиений Л аппроксимируем полиномом второй степени

Ттах (N) - Tmaxi + «1

+ fl.

(--- ч

\ N Nkil

где Ттах 1 соответствует максимальной температуре при числе элементов тепловой схемы замещения, равном Nkt- Коэффициенты fli, flj определяются из решения системы линейных уравнений

+ 01

тахг

maxi

+ fl.

Ттахз ~ Tmaxi + fl2 /--- ----]

\ Nk2