
 |
|
Главная Оптические магистрали [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [ 105 ] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] превышает 1 пФ. После этого необходимо либо уменьшить R, либо применить высокочастотную коррекцию. Сравнение этих двух методов будет проведено в гл. 14. 12.5.3. Переходное время На высоких частотах изменения фототока не успевают за изменениями модулированного оптического излучения. Рассмотрим движение носителей в области дрейфа. В электрическом поле родившиеся носители достигают средней дрейфовой скорости Удр за очень короткое время - обычно доли пико-секунды. В низких полях дрейфовая скорость пропорциональна напряженности поля Е, но по мере роста напряженности достигается насыщение скорости дрейфа. Поле насыщения обычно составляет около 10" В/м. На рис. 12.12 представлена зависимость скорости дрейфа от напряженности для некоторых полупроводников. Будем считать, что поле смещения фотодиода достаточно велико, чтобы поддерживать насыщение скорости носителей в дрейфовой области (см. рис. 12.6). Смысл этого допущения при напряжении смещения Уо и концентрации примесей в области дрейфа Лдр следующий. Ясно, что мы требуем V>Esw.. (12.5.5) Так, для кремниевого диода с дрейфовой областью 50 мкм напряжение смещения должно превышать 10" В/м-50 мкм = 50 В. В соответствии с (7.6.2) для л-типа легирования области электрическое поле изменяется линейно: d£/dx= елдр/ево- const (12.5.6) и полное изменение Е определяется выражением АЕ = еЛдр кУг/ебй. (12.5.7) Имея в виду кремниевый диод, условимся, что изменение £ не должно выходить за пределы 1,5x10" В/м на p+v-переходе и 1,0x10® В/м на Ос/, м/с Рис. 12.12. Зависимость скорости дрейфа носителей от напряженности электрического поля, показывающая, что при высокой напряженности наблюдается насыщение. Должно быть понятно, что скорость дрейфа снижается прн увеличении степени легирования нлн при высокой концентрации дефектов, а также с рос том температуры
10 Е,8/м vn+-nepexofle. При этом обеспечивается насыщение скорости носителей во всей области w. Тогда АЕ < 0,5 X 10* В/м, а при е = 12 и = 50 мкм согласно формуле (12.5.7) Лдр < 6,5 X 10* м-*. Необходимое напряжение составляет 62,5 В. Чтобы обсудить действие переходного времени, предположим, что импульс оптической мощности создает электрон-дырочных пар на /7+-краю обедненной области. Дырки сразу же собираются р+-матери-алом, в то время как электроны дрейфуют через обедненный слой за время <др, которое зависит от электронной скорости насыщения: /др = у„ (12.5.8) где / ж - размер обедненной области. Затем они собираются л+-слоем. Движение заряда вызывает ток. Общий переносимый заряд есть Ne, так что i(t)Ne/tp = NexJl (12.5.9) Для О < / < <др, как показано на рис. 12.13, а. Если носители рождаются на л+-краю обедненного слоя, переходное время и ток определяются скоростью насыщения дырок, как показано на рис. 12.13,6. Рассмотрим теперь, что произойдет, если электрон-дырочные пары будут рождаться в середине обедненного слоя. Электроны дают вклад в ток {Nevjl) за время (u)2/2v), а дырки дают вклад в ток {Ne\Jl) за время (112\), где - скорость насыщения для дырок. Аналогичные соображения можно привести и для носителей, рождаемых в любом месте обедненного слоя. Когда рождение носителей однородно по всей области, ожидается треугольная характеристика, показанная на рис. 12.13, в. Расчет, учитывающий экспоненциальное затухание оптической мощности и, следовательно, скорости рождения носителей, дает импульсную характеристику, приведенную на i(tl Ne\/l 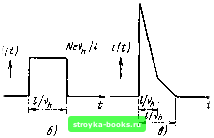 Однородмае •украшение V. носителей \ Освещение: V р-стороны {п-стороны Рис. 12.13. Теоретические импульсные характеристики при различных условиях освещения: а - когда электрон-дырочные пары рождаются только в р+-области обедненного слоя; б - когда электрон-дырочиые пары рождаютси только в п+-областн обедненного слоя; в - однородное рождение носителей; г - рождение носителей экспоненциально меняется по обедиеииому слою рис. 12.13, г. Ожидаемая полуширина импульса тока немного меньше времени пересечения электронами обедненного слоя. Для кремниевого диода при \g = 10* м/с и = 50 мкм время (/др)е = 0,5 не. Диффузия носителей в обедненном слое расширяет импульсную характеристику до времени рекомбинации. Оно едва ли будет менее 10 не. Поэтому важно удерживать ток в пределах этого «диффузионного хвоста». Рассмотрим, как переходное время влияет на характеристику диода при синусоидальной модуляции оптического излучения Ф (О - Фо (1 + sin (оО. (12.5.10) где т - коэффициент модуляции. Проведем формальный анализ для простого случая, когда носители рождаются только у /?+-края обедненного слоя, т. е. в начале координаты х рис. 12.5. Положим, скорость рождения носителей No{\ -f m sin со/). Эти носите/ти (электроны) дрейфуют через обедненный слой со скоростью насыщения для электронов v. Это означает, что в элементе dx на расстоянии х можно ожидать появления тех электронов, которые были рождены на (x/v) секунд ранее за интервал времени dt ~ dx/v. Это будет jVo [1 -f m sin io {t - xl\p)\ (dx/ve), так что полное число будет определяться выражением [1 +т sin (О (< - x/Vp) dx = No I I {cos (I) (t - llVg) - COS (at) ~ , , 2inVe - co/ . , , ,n s 1 H--- sin-sin (o(; - 2vJ ш1 2v„ где / - размер обедненной области. Полный ток / - Nexjl и может быть записан 1 = /„[1 + т sin (at+ ((>)]= No е \l + + т "f"") sin2/(/-„p/2) (12.5.11) (12.5.9). (12.5.12) где сделали подстановку / = (о/2л и = IIv. Ясно, что на высоких частотах характеристика падает I (/) т sin (я/<др) / (0) т nftfp (12.5.13) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [ 105 ] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] 0.0014 |