
 |
|
Главная Оптические магистрали [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [ 12 ] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] Применим (2.1.21) к частному случаю цилиндрического волокна, в котором показатель преломления радиально симметричен. Ограничимся рассмотрением меридиональных лучей, и, кроме того, лишь тех из них, которые всегда остаются почти параллельными оптической оси волокна. Это так называемое параксиальное лучевое приближение, которое позволяет нам аппроксимировать ds расстоянием вдоль оси d2. Тогда (2.1.21) принимает вид d4dz = (Уп) (dn/dr), (2.1.22) где теперь г - расстояние луча от оптической оси, а z - расстояние, измеряемое вдоль оси. Легко показать, что параболический профиль показателя преломления обеспечивает синусоидальный закон изменения г от Z. Пусть, например. п (г) = \ а ! при г<а, (2.1.23) /1о(1 - А) = л(а) при га. где «о - показатель преломления на оси; а - радиус сердцевины волокна, а А = Ыо - « (а)1/«о (2.1.24) - полное относительное изменение показателя преломления сердцевины. Дифференцирование (2.1.23) приводит к выражению dnldr = - (2«ог/а) А. (2.1.25) Ограничившись в дальнейшем рассмотрением только лучей, расположенных близко к оси, можно предположить, что По/"1 ~ 1- Тогда уравнение (2.1.22) принимает вид dV/dz- » - (2г/а2) А. (2.1.26) Если теперь рассмотреть лучи, которые вводятся в волокно таким образом, что г = Го, а dridz = Го в точке z = О, то интегрирование уравнения (2.1.26) даст следующее уравнение траектории луча; г = Го COS (2А) /2 ±. + - s.n (2А) /2 ±,. (2Д.27) На рис. 2.7 приведены траектории двух групп таких лучей при Го = О н г6 = 0. Все они не имеют дисперсии (не диспергируют). Если попытаться ослабить условия параксиального приближения, то это приведет к значительному усложнению уравнений. Можно, однако, показать (см. [2.2]), что все меридиональные лучи не испытывают дисперсии, если профиль показателя преломления имеет вид п (г) ~ По sch аг » Ло 1 -а* г*+ - «**+ 2 24 (2.1.28) Приведенное выше разложение профиля показателя преломления в ряд показывает, что параболический закон является первым приближением к требуемому, если принять А = ((xaf/2. В случае косых лучей не существует такого закона изменения профиля показателя преломления, который бы устранил их взаимную дисперсию (независимо от места и угла ввода), а также дисперсию по отношению к меридиональным лучам. Практические аспекты изготовления градиентных волокон будут рассмотрены в гл. 4, а в гл. 6 и приложении 3 вновь вернемся к волне вой и лучевой теориям распространения света в волокне. Покажем, что при идеальном профиле показателя преломления межмодовая дисперсия может быть сделана менее 0,1 не/км. На практике не представляет труда получать хорошие градиентные волокна с величиной межмодовой дисперсии менее 1 нс/км. Однако при этом может оказаться полезной даже грубое изменение профиля показателя преломления. Например, временная дисперсия волокна со скачком показателя преломления, рассмотренного в виде примера в § 2.1.2, может быть уменьшена с 34 по 10 нс/км и менее путем простого сглаживания изменения показателя преломления на границе сердцевины и оболочки. Прежде чем приступить к анализу дисперсии, необходимо принять во внимание еще один источник временной дисперсии в оптических 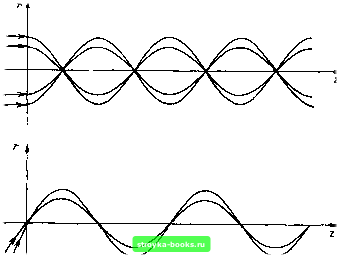 Рнс. 2.7. Траектории меридиональных лучей в волокне с параболическим профилем показателя преломления: предполагается, что профиль показателя преломления имеет вид п(г)=По(1-Д(--1- а все изображенные на рисунке траектории лучей заключены в сердцевине. Имеется в виду, что траектории обладают круговой симметрией относительно горизонтальных осей волокнах. Дело в том, что на самом деле показатель преломления зависит от длины волны. Этот вид дисперсии было бы хорошо назвать хроматической дисперсией, однако ее обычно называют материальной дисперсией. 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ 2.2.1. Показатель преломления объемной среды: теория На распространение электромагнитных волн в прозрачных материалах оказывает влияние их взаимодействие с молекулами среды. Поскольку такое взаимодействие зависит от частоты, то и скорость распространения электромагнитных волн также зависит от частоты: говорят, что материал обладает дисперсией. Одним из проявлений такой дисперсии является уширение коротких световых импульсов при их распространении в диспергирующей среде. Величина уширения пропорциональна ширине спектра импульса и является другим важным фактором, который ограничивает полосу пропускания оптических волокон, В оптике обычно имеют дело с показателем преломления среды п. Он показывает, во сколько раз уменьшается фазовая скорость Vp волны, распространяющейся в данной среде, по сравнению с фазовой скоростью с в вакууме Vp = c/n. (2.2.1) Другая особенность оптики состоит в том, что, начиная с момента зарождения оптики как науки в XVI веке, при описании источников оптического излучения используют не частоту /, а длину волны А, излучаемых колебаний. Это приводит к понятию длины волны в свободном пространстве X = c/f. При распространении колебаний в преломляющей среде длина волны уменьшается до К, причем = Ш (2.2.2) Vp = XJ. (2.2.3) Будем описывать электромагнитную волну частотой f, распространяющуюся через преломляющую среду вдоль оси г, в виде проекции амплитуды электрической составляющей поля на ось х, как действительной части Ех, т. е. E,(z, О = £оехр {-/(coZ-pz)}. (2-2.4) где Eq - постоянная поля; р = 2л/Хт - коэффициент распространения в среде; со = 2я/ - угловая частота волны, а / = - 1. Выражение (2.2.4) описывает плоскую волну, распространяющуюся в объемном материале. Будем полагать, что волна линейно поляризо- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [ 12 ] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] 0.002 |