лим единичные векторы ir, 1,,, iz в каждом из трех направлений координат в любой точке г на траектории луча, В таком случае

T-rlr + ziz, откуда следует dr dr

(П3.2)

ds ds ds ds ds

Далее, кач это видно из рис, П3.1, справедливы следующие соотношепия: dir . d(p

(ПЗ.З)

ds ds

f ds d<p

(П3.4а) (П3.46)

Следовательно, dr dr

\z + r

(П3,4в)

(П3.5)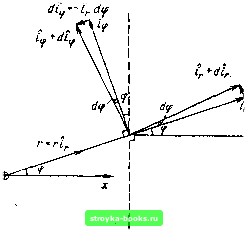

dtrlifdif

Рис. П3.1. Единичные векторы в точке Q(r, ф)

Рисунок показывает, что между единичными векторами ir и (ц, имеют место соотношения типа дифференциала

diidV), (П3.4а)

dl==-id4,. (П3.46)

Единичный вектор в направлении оси г ие зависит от положения, и потому

dl = G.

(П:}.4в)

Перепишем теперь исходное уравнение (П3.1) d

("17

и сделаем подстановку, приняв во внимание, что dnldi и dndz обращаются в нуль

d dr \ d / dtp \ d dz \ dn nr-r- i,„ +

dr \ d I

dz n-

(П3.6)

Осуществив почленное дифференцирование уравнения (П3.6), получим

dr \

dr dlj d

ds ds

\ . d dz \ .

X-- -\--I n- U + n

ds ds \ ds

ds dz diz

d(p \ ds

ds ds dr

Исходя из этого и испо.тьзуя соотношении (П3.4), окончательно находим

d(f \

dr da.

ds I dz \

d£\2

I ds )

dn dr

(П3.7)

Группируя выражения, содержащиеся при ir, i и i, и приравнивая каждую из групп по отдельности правой части, получаем: для ir

d I

ds \

ds \ ds j \ ds j

для i

n

dr d<f

ds ds

nr

d(f ) dT

dn dr

для tz d

(П3.8)

(П3.9)

(П3.10)

Из уравнения (ПЗЛО) следует, что п (dzlds) - величина постоянная, определяемая положением и направлением луча р. точке входа в волокно. Согласно рис. 6.3, а направление и положение луча в этой точке определяются координатами («о, Ро. Yo) и (о. Фо. 0) соответственно. Таким образом.

(11.)

\ ds Д=.0

.-cosYo

(ПЗ.М)

dz ds

где £ - так называемый «энергетический» параметр луча. 16*

(П3.12)

ifsmac,