
 |
|
Главная Оптические магистрали [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [ 20 ] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] спектра, непосредственно используя для этого выражения (2.4.1) ... ...(2.4.3). Кроме ТОГО, ширину спектра можно определить либо через разброс длин волн, содержащихся в свете, либо на основе разброса угловых частот. Пусть полная мощность, излучаемая данным источником в некоторый момент времени, равна Ф, причем Фо= \ Ф<о(о))а). (2.4.4) .-(Ж Здесь Ф(й (ю) представляет спектральн}Ю плотность мощности в виде функции оптической угловой частоты. Тогда среднее значение оптической угловой частоты (о будет равно: ы = J <Ьф (ш) do), (2.4.5) а среднеквадратическое значение ширины спектральной линии будет описываться выражением а = J-Г(й«Ф(ш)а) -ш. (2.4.6) Фо J Аналогично можно определить среднюю длину волны, излучаемую источником к, и выразить среднеквадратическую ширину спектральной линии Ох через длину волны. Это можно сделать следующим образом: Фо = ]фх{к)с1к, (2 АЛ) где Фх, (к) - спектральная плотность мощности как функция длины волны (Фх (к) измеряется в Вт/м, а Ф (со) - в Вт-с). Далее находим к= - \кФк{к)с1к. (2.4.8) И, наконец, окончательно получаем = J- {кФх{к) dk-J. (2.4.9) То J Важно подчеркнуть, что величина а характеризует разброс длин волн, а Ощ - угловых частот. Предположим теперь, что импульс уширяется под влиянием как межмодовой, так и материальной дисперсий, что оба механизма уши-рения взаимно независимы и независимо приводят к формированию приблизительно гауссовых импульсов, имеющих среднеквадратиче-ские длительности, равные соответственно Oi и а.. Оба механизма уши-рения снова будут объединяться, чтобы сформировать импульс, который останется приблизите.аьно гауссовым по форме и среднеквадратическая длительность а которого будет определяться выражением (2.4.10) Если передаваемый импульс не бесконечно короткий, имеет гауссову форму и среднеквадратическую длительность а,,, то среднеквадратическая длительность результирующего импульса будет равна (2.4.11) По сравнению с общей длительностью импульса, обусловленной межмодовой дисперсией, которая была рассмотрена в § 2.1, величина а, зависит от того, каким образом оптическая мощность распределяется между различными траекториями лучей. Величина а. может быть найдена с помощью формулы (2.2.41) Ох = dk с где у„ = Ом/О) = ах.Д. dN d(i) O(o/ft) = (2.4.12) Установим взаимосвязь между среднеквадратической длительностью импульса о и его длительностью т на уровне 0,5, а также другими его параметрами для ряда приведенных на рис. 2.16 гипотетических импульсов, имеющих различные аналитические описания своей формы. Приведенные ниже соотношения получены простым вычислением по формуле (2.4.3) для каждого случая: а) прямоугольный импульс т = ДГ, а= AT/2V3 = 0,289ДГ= 0,289т; б) треугольный импульс т=0,5ДГ, а- ДГ/2Кб" = 0,204ДГ= 0,408т; в) пилообразный импульс т = 0,5ДГ, а=ДГ/31/2 = 0,236ДГ= 0.471т; (2.4.13) (2.4.14) (2.4.15) 67 г) экспоненциальный импульс т==0,693т„ ст = т„ = 1,44т; (2.4.16) д) гауссов импульс T = (log2)/2 т„ = 0,833т„ СТ = г,/21/2" =-0,354х,-0,425т; (2.4.17) е) усеченный лоренцевский импульс CT = -X/tg-iXi/2, (2.4.18) где X = ЛТ/т. Отметим, что а оо при X оо. Некоторые из этих соотношений будут использованы в дальнейшем. Их доказательство представляется читателю в качестве упражнений. фft) 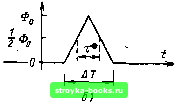 0 I- 1ф , 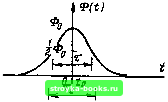 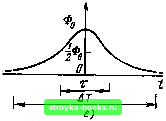 Рис. 2.16. Среднеквадратическая длительность импульсов разной формы: а-прямоугольный импульс (о=т/У12); б - треугольный импульс {о=т/У5); в - пилообразный импульс (о=тУ2/3); г - экспоненциальный импульс {Ф(<) = =Фоехр[-(<-<о)/тв], о=1,44т); 3-гауссов импульс (Ф(0=Фоехр[-(<- - ад2<т2], о=0,425т); е - лоренцевский импульс (Ф(0=Фв/П+4(/-<о)т1) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [ 20 ] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] 0.0012 |