в этом параграфе на более высоком уровне будет рассмотрена теория распространения света в такой неоднородной среде.

В идеальном случае для решения поставленной задачи следовало бы найти решения уравнений Максвелла для градиентного волокна и затем по ним определить дисперсионные свойства волокна. Однако любой общий анализ задачи вскоре становится трудноосуществимым.

В Приложении 1 отмечается, что для получения волнового уравнения (П1.2) использована подстановка

div Е = div (О/гг) = 0.

В неоднородной среде, когда величина г,, зависит от координат, это предположение становится несправедливым, так как

div(D/e,eo) = -V(D/e,) =

VD+DV

(6.1.1)

Это выражение преобразуется к следующему виду, если учесть, что VD = О и подставить п Уе,.,

•Ve,=--VH-

Тогда волновое уравнение запишется следующим образом:

VE-f V

л2 d-i Е

(6.1.2)

(6.1.3)

В уравнении для Н также появляется поправка (1/л) V (л).

Во всех представляющих практический интерес градиентных волокнах величина V (л*) достаточно мала, что делает эти новые слагаемые приближенно малыми и не оказывающими существенного влияния на характеристики распространения электромагнитных волн в волокне. Будем это иметь в виду в дальнейшем. Таким образом, следует найти решения уравнения (П1.2, г).

VV -

с2 dfi

= 0,

(6.1.4)

где W обозначает Е или Н, а л является медленно изменяющейся функцией радиальной координаты рассматриваемой точки.

Точные решения уравнения (6.1.4) можно получить в виде известных функций, если профиль показателя преломления сердцевины принимает параболический вид

л(г)=Ло[1~2Л(г/а)/2 при г<а и

л(г) = Ло[1-2Л1/2 = Ле при г>а.

(6.1.5)

Напомним, что - показатель преломления на оси волокна, и при А < 1 можно записать

А = {п1-пс}/2п1 {щ--п,)!По. (6.1.6)

Вместо того, чтобы отдельно разобрать этот частный случай, можно рассмотреть обобщенное представление осесимметричного профиля показателя преломления в таком виде:

п{г) = По[1-2А/(г)1/2 при г<а, п(г) = По[1 -2А/2 = „ при г>а.

(6.1.7)

где/(0) = О и / (а) 1.

Для описания так называемого а-профиля широко использовалась особая функция

/(г).= (,-/а)°. (6.1.8)

Здесь параметр профиля а может принимать значения от единицы до бесконечности. Параболический закон изменения профиля показателя преломления вида (6.1.5) получается подстановкой а 2, а случай а = оо можно рассматривать как предельный соответствующий ступенчатому профилю. Однако необходимо отдавать себе отчет в том, что подстановка а=оо в уравнения (6.1.7) и (6.1.8) приводит к определению А с помощью выражения (6.1.6), которое несколько отличается от определения, данного в гл. 5. Сравнение выражения (6.1.6) с (5.4.2) сделает это более понятным. В предположении малости А это различие становится пренебрежимо малым. Ряд примеров а-профилей изображен на рис. 6.1.

6.1.2. Приближенное решение

В приложении 1 отмечается, что решение волнового уравнения вида (П1.2) или (6.1.4) требует, чтобы радиальные распределения электрических и магнитных полей ¥г удовлетворяли условию (П1.7), а именно

dr г dr

.пЧг)-Р

V,= 0. (6.1.9)

В этом уравнении р - постоянная распространения, которая характеризует периодичность полей в направлении оси волокна с помощью экспоненты ехр (/Рг); k - целое число, которое учитывает периодичность полей в азимутальном направлении посредством члена ехр х x(/W).

На первом этапе решения уравнения (6.1.9) исключим слагаемое dWr/dr. Этого можно достичь путем подстановки

U = rf%. (6.1.10)

в этом случае уравнение (6.1.9) принимает вид

и=о.

Обозначим выражение в квадратных скобках через К, т. е.

(6,1.11)

(6.1.12)

Анализ уравнения (6.1.12) показывает, что на определенных угловых частотах со для света, распространяющегося в виде моды, имеющей данную постоянную распространения р, будут существовать некоторые области в волокне, где К - действительная величина, и другие области, где К - мнимая величина. Из рис. 6.2 следует, что К принимает действительные значения внутри области ограниченной и Гг, для которой справедливо неравенство

:I pii:ziZl. (6.1.13)

В Прилонсении 2 показано, что внутри этой области (распределения полей) поля изменяются периодически в зависимости от радиуса, в то время как вне этих границ они уменьшаются экспоненциально. По аналогии с рассмотрением, приведенным в § 5.2, свяжем эти периодические распределения полей, ограниченные цилиндрической областью между радиусами н Tj, со световодными модами и уменьшающимися затухающими полями вне этих радиусов.

При Л = 0 не существует никакой границы ниже н периодический характер полей световодных мод расширяется вплоть до оси волокна. Как и ранее, можно полагать, что такие моды соответствуют меридиональным лучам. В этом случае поля обладают радиальной симметрией.

Необходимо чтобы периодический характер распределений полей между и Гг был согласован с затухающими полями вне этих границ, а это означает, что только определенные дискретные значения постоянной распространения р будут удовлетворять граничным условиям и, следовательно, обуславливать возможные моды распространения. Обозначим, как и прежде.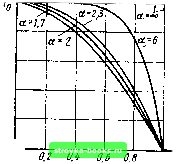

10 г/а

Рис. 6.1. а-профили показателей преломления градиентных волокон:

Профили показателей преломления даны при а=1,7; 2,0; 2,3; 6,0 и а=оо (ступенчатый профиль)