
 |
|
Главная Оптические магистрали [0] [1] [2] [3] [ 4 ] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] Времл 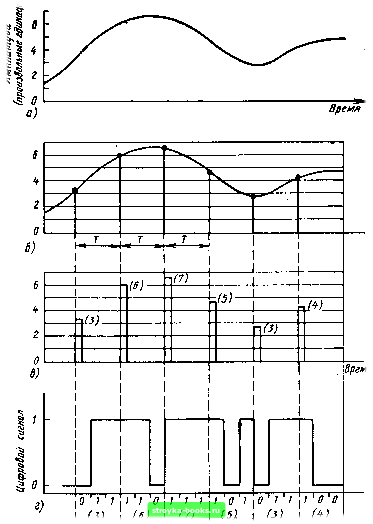 ВргмА Рис, 1.4. Основные этапы преобразования аналогового сигнала в цифровой: а - аналоговый сигнал; б - аналоговый сигнал, днскретнзируемый по времени с интервалом Г; в - днскретнзироваииый сигнал, квантуемый по амплитуде иа 2-8 уровней; г - цифровой двоичный сигнал, полученный нз дискретного по времени и квантованного по состояниям сигнала в результате кодирования прн 3 бнт/отсчет ла (рис. 1.4, а) дискретным (рис. 1.4, в) необходимо, чтобы отсчетов (дискретизации) /«, равная \1Т, где Т - интервал дискретизации, была, по крайней мере, в 2 раза больше наивысшей частоты fm, содержащейся в спектре дискретизируемого сигнала. При выполнении этого условия, впервые сформулированного Найквистом, исходный аналоговый сигнал может быть просто восстановлен путем пропускания дискретизированного сигнала через фильтр нижних частот, пропускающий все частоты ниже/т. Диапазон частот от О до представляет собой ширину спектра исходного сигнала, которую будем обозначать А/. Следовательно, в нашем случае Д/ = f- Таким образом, частота дискретизации должна выбираться из условия > 2Д/. Следующим шагом является постановка в соответствие каждому значению отсчета сигнала одного из конечных значений уровней амплитуды сигнала (т. е. квантование сигнала по уровню). В принципе амплитуда отсчета может принимать любое значение из непрерывного интервала изменений дискретизируемого сигнала. Необходимо, однако, помнить, что на практике всегда имеют место случайные флуктуации (шумы), которые накладываются на интересующее нас колебание, отображающее сигнал. Это так называемый системный шум, который делает бесполезными попытки обнаружить разность между двумя уровнями сигнала, если она по величине соизмерима со средневадратиче-ским значением флуктуации. В действительности, именно отношение максимальной величины сигнала (As) к среднеквадратическому значению шума {An) и определяет число уровней квантования, которое необходимо для достаточно точного представления исходного сигнала. Пусть число уровней квантования равно т. Тогда каждый отсчет сигнала потребует для своего кодирования = Xogm двоичных цифр. При декодировании полученного цифрового сигнала (рис. 1.4, г) и восстановлении исходного аналогового сигнала возникают ошибки, обусловленные квантованием. Они приводят к появлению дополнительного шума, известного как шум квантования. Можно показать, что шум квантования сравним по величине или меньше исходного шума квантуемого сигнала при условии, что число уровней квантования больше, чем [1 -f (Лз/ лг)1- Таким образом, чтобы представить исходный аналоговый сигнал, занимающий полосу частот Д/ (Гц) и имеющий динамический диапазон AsIA, в цифровом виде, потребуется минимум В двоичных цифр в секунду (бит/с), где В = 2Д/ log2 [ 1 + {AslAsfVi = Д/ log2 [ 1 + {AslAs)% (1.2.1) На полученный результат можно посмотреть и с иной стороны. Говорят, что канал связи обладает информационной пропускной способностью В (бит/с), если он способен передавать аналоговый сигнал, занимающий полосу частот Д/, и поддерживать на выходе приемника (где отношение сигнал-шум наименьшее) отношение пикового значения сигнала к среднеквадратичному значению шума, равное AslAf. В этом случае величина В также определяется по формуле (1.2.1), известной как формула Шеннона, правильной интерпретации которой было посвящено много дискуссий. В данной главе попытаемся использовать эту формулу для сравнения информационной емкости сигналов разного вида, а также для сравнения между собой различных каналов связи по информационной емкости. В каждом случае скорость передачи информации прямо пропорциональна полосе частот Af, в которой она передается, и логарифмически зависит от минимального значения отношения сигнал-шум (в приемнике). В результате исследования практических каналов связи было установлено, что цифровое кодирование аналогового сигнала обычно требует существенно более высокой скорости передачи информации, чем определяемой выражением (1.2.1). Несколько позже мы проиллюстрируем это на примерах. Аналогично этому объем информации, который можно передать по каналу связи, существенно меньше, чем это предсказывает формула (1.2.1). На практике отношение As/А f, значительно больше единицы и его обычно выражают в децибелах. В этом случае формулу (1.2.1) можно упростить. Допустим, например, что величина отношения As/А f, равна X дБ, т. е. X =- 20 Ig (As/A Тогда формула Шеннона преобразуется к виду В =0,332Х.Д/, (1.2.2) бит/с1 [дБ] [Гц] поскольку Iog2l0 = 3,32, а 1 можно пренебречь в сравнении с (As/А f. В качестве примера рассмотрим теперь количество информации, содержащееся в таких привычных для нас формах ее представления, как книга, грампластинка и магнитная пленка видеомагнитофона с записью телевизионного фильма. Одновременно дадим оценку информационной емкости канала связи, необходимой для прямой передачи звуковой и видеоинформации. 1. Книга. Рассмотрим книгу объемом 100 ООО слов, содержащую, например, 250 страниц, причем допустим, что каждое слово состоит в среднем из пяти букв. При использовании для преобразования текста в цифровую форму наиболее широко используемого кода ASC И, каждая буква кодируется семью двоичны.ми цифрами. Таким образом, на каждую букву приходится 2 = 128 бит, причем учитываются все строчные и прописные буквы, цифры, промежутки между словами и знаки препинания. Тогда общий объем содержащейся в книге информации составит 3,5 Мбит. 2. Звуковой канал. Для обеспечения разборчивости речи требуется полоса частот около 3 кГц, лежащая в диапазоне от 300 Гц до 3,4 кГц для обычной стандартной телефонной сети. При этом результирующее отношение сигнал-шум должно быть более 30 дБ (As/А f,= = 31,6). Воспользовавшись формулами Найквиста и Шеннона, получим значение скорости передачи информации, равное 30 кбит/с, при условии, что минимальная частота дискретизации составляет 6 кГц, а каждая выборка кодируется, по крайней мере, 5-разрядным словом. [0] [1] [2] [3] [ 4 ] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] 0.0013 |