
 |
|
Главная Оптические магистрали [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [ 59 ] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165]  Затухающая волна  Сдетодвдная \3amyfaw-1 Полна S майа и мода, щая волна\ вдолочне уточни. 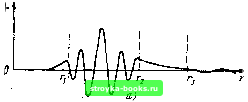 Затухающая волна Ьтупенчатыи профиль СВетоводшмедсЬату Волна В и мода утечки тн!-\оволочне щал волна  Рис. 6.9. Моды утечки в градиентном (а) и ступенчатом (б) волокне. Графики, аналогичные приведенным на рнс. 6.2. показывают области, в которых моды распространения могут быть найдены при кфо и >Э=>Р ftVo. Если волна введена в область распространения, заключенную между радиусами /-, и (между Vi и а для ступенчатого волокна), она не в состоянии непосредственно преобразоваться в иеканализируемую волну в оболочке из-за наличия области затухания, расположенной между и г,. Следовательно, она может распространяться в серлцев1сн<> па значительное расстояние до тех пор. пока не покинет волокно ния волноводных потерь и потерь от микроизгибов, на которые указывалось в § 3.1.3, где рассматривали, каким образом неоднородности и неровности поверхности, встречающиеся в световоде, воздействуют на характеристики распространения. Изменения характеристик распространения могут быть следствием изменений структуры материала, изменений радиуса сердцевины или просто изгиба волокна, вызванного внешними силами. Рисунок 6.10 показывает, как образуются небольшие изгибы волокна (микроизгибы) при его укладке на неровной поверхности. Другая причина изменений характеристик волокна может быть связана с его спиральным расположением в многожильном оптическом кабеле. Предполагается, что перечисленные неоднородности очень малы по величине. Большие неоднородности вызывают и большие локальные потери. Если неоднородности имеют место на расстояниях, меньших длины волны, то они приводят к появлению рэлеевского рассеяния (§ 3.1.3). В таком случае небольшая часть переносимой всеми световодными модами мощности может быть рассеяна в виде ненаправленного излучения. Неоднородности, которые по своим размерам превышают длину волиы излучения, не способны создать такое рассеяние, однако они могут вызвать обмен энергией между соседними модами. В случае, когда моды располагаются вблизи частоты отсечки, это может привести к переносу энергии от световодных мод высоких порядков к затухающим или неканализируемым модам, которые затем уходят за пределы волокна. Если принять во внимание, что в одном километре волокна укладывается около 10 длин волн, то становится ясно, что даже очень малые возмущения, создаваемые в световоде неоднородио-стями, будут достаточными для нарушения характеристик распространения света в нем, если эти неоднородности имеют место на значительной части волокна. Обмен энергией между модами происходит лучше всего тогда, когда картины по-тей мод перекрываются в значительной степени, причем неоднородности наиболее эффективно содействуют этому обмену, если их периодичность равна периоду биений между этими двумя модами. Распределенное давление \ I I I I Оболочка иииличпи - - Сердцевина ------ ~------Щ Рис. 6.10. Микроизгиб волокна, создаваемый малоразмерным предметом, находящимся на плоской поверхности. Если оказываемое на волокно давление невелико, естественная жесткость самого волокна н податливость его пластикового покрытия сгладят резкое изменение поверхности на расстоянии в несколько миллиметров Последнее утверждение можно проиллюстрировать следующим образом. Пусть неоднородности в световоде будут периодическими и им соответствует пространственная длина волны Л и пусть постоянные распространения рассматриваемых двух мод равны Pj и р. Тогда взаимодействие этих мод будет самым сильным при выполнении условия Л = 2я/ р..-Р; = 2я/Ар. (6.6.2) Взаимодействие мод, которые имеют значительно отличающиеся постоянные распространения, требует наличия периодических неоднородностей с более короткой пространственной длиной волны. Обычно неоднородности в волокне распределены равномерно по размерам, что приводит к взаимодействию мод в широком диапазоне. Однако путем тщательного контроля процессов изготовления волокна и проектирования оптических кабелей нз них было бы возможно исключить очень быстрые изменения свойств волокна и таким образом предотвратить взаимодействие мод, постоянные распространения которых существенно разнесены друг от друга. В частности, обычно хотят предотвратить преобразование мод высокого порядка, близких к частоте отсечки, в неканализируемые моды, поскольку такое взаимодействие сильно увеличит затухание в волокне. Итак, моды стремятся распространяться в виде модовых групп, причем в каждой группе все моды имеют очень сходные постоянные распространения. В любой такой группе моды могут хорошо обмениваться энергией между собой без воздействия на характеристики волокна. Однако взаимодействие между модами разных групп было бы более опасным. Было показано, что постоянная распространения р, для мод в группе q определяется выражением Pq = Ро 1-2Л 2а/(а-; 2) (6.1.40) где Ро - постоянная распространения плоских волн типа ТЕМ в материале, характеристики которого соответствуют материалу оси волокна; а - параметр профиля показателя преломления; А - относительная разность показателен преломления сердцевины и оболочки; Q - общее число световодных мод в группе. Для сердцевины радиусом а имеем «Д il/2 (6.1.41) Интервал между соседними модами в группе будет равен Ар = Р,-р<,-1 = - (а + 2) q \(а-2)/(а+2) - -гд/- \ Q / 2а/(а-- 2) -1/2 I Q аД (а-2)/(а--2) (6.6.3) 185 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [ 59 ] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] 0.0013 |