
 |
|
Главная Оптические магистрали [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [ 77 ] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] (Po/h) AS О..Л0 -1,5... -J...B,S 0.2 -10...0J 0,05 ЮМГц /д, ЮОМГц 1ГГц Частота модуляции Рис. 8.13. Зависимость выходной мощности светоизлучающего диода от частоты модуляции. Сплошная кривая соответствует выражению (3.7.35) при /т--1/2яТр=25 МГц (Tp-6.4 не). Кружками обозначены экспе риментальные точки 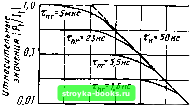 1МГц ЮМГц ЮОМГн Частота модуляции Рис. 8.14. Кажущееся увеличение ши-рокополосности светои,элучающего диода прн увеличении скорости бе-зызлучательной рекомбинации. (Оно достигается лишь за счет падения низкочастотной квантовой эффективности. Высокочастотная квантовая эффективность может быть увеличена только при уменьшении Ти.) квантовая эффективность. В случае арсенида галлия это происходит при концентрации примеси порядка м-*, при этом т„ » 10 не. То есть частоты модуляции значительно выше 20 МГц могут быть достигнуты только за счет квантовой эффективности. Как будет показано в§ 9.3, в 4 раза большую полосу модуляции без снижения эффективности удается получить в светоизлучающих диодах на InGaAsP/InP. На рис. 8.5, б показано, что они излучают в области 1,3 или 1,5 мкм. ЗАДАЧИ 8.1. Предполагая, что функции плотности состояний определяются выражениями (8.2.5) и (8.2.6). а распределения электронов в зоне проводимости и дырок в валентной зоне-распределением Больцмана [формулы (7.2.4) и (7.2.5)1, показать, что rt (е) и р (е) достигают максимальных значений при энергии (fe7"2) от края зоны. Доказать, что диапазон энергий, при которых п {?) и р (е) превышают (1/"\/2) от максимального значения, составляет 1,1 кТ. 8.2. Показать, что спектральное распределение спонтанного излучения (8.2.12) вытекает из (10.2.13), когда функции плотности состояний 5(8) и S„ (81) предполагаются постоянными, а функции Ферми и (1 - f j) - экспоненциальными. 8.3. Показать, что теоретическое спектральное распределение мощности (8.2.12) достигает максимального значения при энергии фотона (в - кТ) и имеет полуширину 2,4 кТ. 8.4. Предполагая, что спектральные характеристики светоизлучающего диода (рис. 8.5) относятся к 300 К, рассчитать сггектральную ширину в единицах 7" для каждого случая. 8.5. Преобразовать (2.1.13) так. чтобы оно выражало долю излучения плоского изотропного источника в среде с показателем преломления и, которая будет распространяться по волокну, имеющему показатель преломления сердцевины /п,, а оболочки rtj. 8.6. Используя результаты решения задачи 8.5, рассчитать общий коэффициент связи волокна и светоизлучающего диода при коэффициенте преломления полупроводника 3.7, а сердцевины и покрытия 1,460 и 1,455 соответственно. Считать, что диаметр сердцевины волокна превышает размер излучающей области и волокио соединено с поверхностью полупроводника клемм, имеющим тот же самый показатель ггреломления, что и у сердцевины. Как изменится коэффициент связи, если плоскую поверхность полупроводника заменить выпуклой или вогнутой? 8.7. Источник малого размера дает излучение с угловым распределением / (9) /о cose, где а > 1 и 6 - угол относительно нормали к поверхности. Сравнить коэффициент связи с волокном такого источника и Ламбертова источника, для которого а - \. 8.8. Преобразовать формулы (8.7.26) для случая высоких частот (йТр> 1. РЕЗЮМЕ Эффективность инжекционной люминесценции зависит от преобладания прямой зона - зонной излучательной рекомбинации над другими механизмами рекомбинации, показанными на рис. 8.1. Это реализуется в прямозонном материале. Внутренняя квантовая эффективность где т„ 1 /г (п„о + Ртл -т Дп)- Когда преобладает безызлучательная рекомбинация на ловушках (10>*/Wj,) м-с. Длина волны оптического излучения X ж (1,24/е) мкм- эВ при энергии фотона 1,5 ...3,5 кТ. Потери, вызванные переизлучением, поглощением, френелевским отражением и полным внутренним отражением от поверхности полупроводника снижают достижимую мощность: /7-: 2/п(1 + nf. Иммерсия и просветление могут уменьшить френелевские потери. Внешняя квантовая эффективность Лвнеш = /Пвпеш- Онтическая выходная мощность первоначально пропорциональна питающему току, но затем появляется тенденция к насыщению. Генерация оптического излучения снижается с ростом температуры. На рис. 8.10 показан диод конструкции Барраса, имеющий малую излучающую поверхность и высокую яркость. При размере источника меньше диаметра сердцевины волокна передаваемую в волокно мощность можно увеличить, используя линзовые согласующие устройства, которые обеспечивают максимальный коэффициент связи Т)во., Лвнут ("Г - rt2)/2n Типичная частотная характеристика 1 Pl/-/. I 1 где 1/т„==(1/Ти)+(1/Тб). 238 Уменьшение Tq приводит к уменьшению Тр и поднимает частотную характеристику за счет снижения квантовой эффективности. 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР 9.1. ГЕТЕРОПЕРЕХОДЫ 9.1.1. Типы гетеропереходов В гл. 7 и 8 обсуждались р-п-переходы, образованные введением пе-больнюго количества ггримесей в полупроводниковый материал. Они могут быть названы гомопереходами. Однако, как показано на рис. 7.3 и 7.4, существуют совершенно различные гюлупроводнико-вые материалы, которые тем не менее имеют одинаковые или почти одинаковые постоянные кристаллической реп1етки. Поэтому они могут образовывать один монокристалл. На границе между ними меняется ширина запрещенной зоны, электронное сродство, диэлектрическая проницаемость и другие свойства. Такие переходы между полупроводниками, имеющими согласованные решетки, но различные свойства, называются гетеропереходами. В гетеропереходах каждый из [юлупроводников может быть р-типа или п-типа. Таким образом, могут быть реализованы четыре комбинации. Если использовать для широкозонного материала обозначения прописной буквой или Р, а для узко.зонного - строчной п или р, то возможны следующие переходы с различными свойствами: п - N, р -= Р, п Р и Р п. Кроме того, могут появиться различия, обусловленные разным электронным сродством. Система электронных уровней в двух изолированных материалах, образующих гетеропереход, [юказана на рис. 9.1. Эта система соответствует свободным GaAs и GaAIAs, причем материал с узкой зоной имеет большее электронное сродство, а различие мало, так как As присутствует в обоих полупроводниках. Для плоского гетероперехода, как и для обсуждавшегося в § 7.6 гомоперехода, электростатический потенциал V (х) определяется одномерным уравнением Пуассона dV/dx -ip{x)/eeo). (9.1.1) где р - локальная концентрация зарядов, гг - диэлектрическая проницаемость материала, х - координата, перпендикулярная переходу. Изменение градиента потенциала указывает на наличие некомпенсированного заряда. Вакуумный уровень остается непрерывным но Это утверждение не совсем точно. См., например, N. R. Frensley, Н. Кгое-mer.- Theory of the energv-band lineup at an abrupt semiconductor heteroiuncti-on, Phys. Rev., BI6, 2642-2652 (1977). [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [ 77 ] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] 0.0013 |