передачи можно разделить на три большие группы (на рис. 1.2, слева простейшие из представителей этих групп выделены штриховыми линиями).

К первой группе относятся полосковые линии, функционирующие в основном на поперечных (Т-волны) или квазипо-перечных волнах (область / на рис. 1.2). Наиболее общим примером такой линии является симметричная полосковая линия (СПЛ) с проводниками ограниченной ширины (СПЛО). Эта линия замечательна тем, что при увеличении поперечных размеров среднего проводника до бесконечности она

.-----1,-,

МодельМ

а X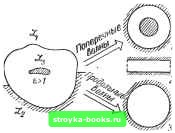

Рис. 1.2

переходит в несимметричную полосковую линию (НПЛ), а при исключении его - в двухпроводную ленточную линию (ЛЛ). Кроме этого, существуют различные промежуточные вариантвг СПЛО. Например, выбрав ширину крайних проводников намного большей ширины среднего проводника, получим модель известной СПЛ. Разнесение проводников таких линий в слоях диэлектрика позволяет решать задачи о передаче СВЧ энергии в вертикальном направлении *).

Ко второй группе относятся симметричные щелевые линии (СЩЛ) с проводниками, расположенными в плоскости слоя диэлектрика (область на рис. 1.2).

Для этих линий характерно присутствие продольной составляющей компоненты электромагнитного поля. В ОИС данный класс линий необходим для реализации пространственных связей (в основном межэтажных) и параллельного включения полупроводниковых (активных и пассивных) приборов.

Роль соединительных узлов между этажами ОИС могут выполнять оптические или квазиоптические элементы (см., например, [11]).

к третьей группе относятся несимметричные линии передачи, имеющие, как правило, сложную структуру электромагнитного поля (гибридные волны). Ключевая структура Б виде несимметричной щелевой линии (НЩЛ) показана на рис. 1.2 (область /). Для НЩЛ характерно расположение токонесущих проводников в разных слоях диэлектрика, что позволяет не только реализовывать пространственные связи с другими типами линии, но и организовывать активные полупроводниковые структуры сосредоточенного и (или) распределенного характера.

Совокупность линий, относящихся к трем указанным группам (рис. 1.2, слева), образует основу для создания элементной базы ОИС СВЧ. В одном СВЧ модуле на ОИС, по-видимому, нецелесообразно использовать комбинацию большого числа типов линий. На практике наибольшее распространение получили три типа волн (Т-, Н-, Е-волны); поэтому для их передачи и трансформации обычно достаточно использовать не более трех - пяти типов ЛП в одном устройстве. Чрезмерное увеличение числа ЛП, как правило, не приводит к улучшению электрических характеристик модуля, а сложность технологических операций при изготовлении возрастает. По тем же соображениям нецелесообразно значительно увеличивать число связанных (или могущих оказаться связанными) слоев диэлектриков в одном модуле. В этом случае имеются ограничения по критериям физического характера - возникновение паразитных типов волн ) (поверхностные и объемные волны) в слоях диэлектрика - и технологического - многослойная топология проводников (проблемы точности совмещения фотошаблонов и реализация гальванических элементов связи) ).

Задачи, связанные с созданием САПР ОИС СВЧ, требуют достаточно полного и строгого математического моделирования (модель ЛП), основанного на рассмотрении трех-

*) В особенности такая опасность возникает, когда БЭ изначально предназначен для функционирования на одном из высших типов колебаний. Такой режим в целом ряде случаев является выгодным. Так, например, на высших типах получаются более высокая добротность (открытые резонаторы) и меньшие погонные потери (микрополосковые ЛП); с их помощью можно расширить полосу микрополосковых антенн и мн. др. [6, 7].

) Применение в ОИС СВЧ межслойных гальванических элементов связи является вынужденным и определяется в большей части случаев недостаточно высоким технологическим уровнем изготовления ИС и ОИС. В перспективе ОИС СВЧ будут реализованы с полностью безгальваническими связями, что даст возмолшость разработчику проектировать, в частности, миниатюрные системы для сверхбыстродействующей обработки информации . на СВЧ.

мерных электродинамических структур, переход к которым показан на рис. 1.2 стрелкой. Построение математических моделей, адекватных исходным физическим задачам, обычно представляет весьма трудную задачу. Строгий анализ дисперсионных свойств основной волны в сложных направляющих структурах оказывается непростым даже для ЛП, относящихся к первой группе (основной тип волны - ква-зи-Т-волна). Поэтому для практических целей в проектировании ОИС СВЧ необходимо обращаться к модельным представлениям, использующим различные приближенные граничные условия. В связи с этим необходимо подбирать и способы формализации задачи.

Наибольший интерес представляет метод Олинера, первоначально предложенный в 50-х годах и усовершенствованный позднее [2]. Этот метод позволяет при наличии ряда предположений (одноволновый режим ЛП) и определенных ограничений при его использовании (например, не учитывать излучающие (вытекающие) волны) получать приемлемые для практики результаты [2-4]. Физическую основу эвристического подхода Олинера составляет предположение о том, что энергия рабочей волны (квази-Т-волны или волны другого типа) сконцентрирована в небольшой окрестности токонесущего проводника (регулярной ЛП) или вблизи неоднородности (базового элемента). Предполагается, что распределение полей в поперечном сечении регулярной ЛП мало изменится,если на некотором расстоянии слева и справа от токонесущего проводника поместить идеальные магнитные стенки.

Рассмотрим более общий подход к задачам моделирования квазиоткрытой структуры, приведенной на рис. 1.2 в центре. В зависимости от геометрической формы контуров

-в структуре могут существовать поперечная волна и продольные волны Н-, Е-типа; электродинамический расчет характеристик даже регулярных структур с такими волнами весьма непрост. Однако качественное распределение полей Б линии, как правило, довольно несложно определяется, например, из статической задачи {d/dt=0). Эти знания позволяют в какой-то мере определять соответствие полей для известных волноведущих линий, параметры которых описываются строгими аналитическими выражениями (переход к таким структурам показан на рис. 1.2 стрелками). Исходя из этого, можно найти неизвестные параметры исследуемой линии с помощью следующих соотношений:

Ziz,, бф8ф, (11)