
 |
|
Главная Введение в электрику [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [ 63 ] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] f = 30 Гц. ПРИМЕР: Если синусоида имеет частоту 60 герц, то чему равен ее период? Дано: Решение: f = 60 Гц t = - = - t ? f 60 t = 0,0167 с или 16,7 мс. 12-2. Вопросы 1. Дайте определения следуюгцих величин: а. Пиковое (максимальное) значение; б. Размах синусоиды; в. Эффективное значение; г. Среднеквадратичное значение. 2. Синусоида напряжения имеет пиковое значение 125 вольт. Чему равно эффективное значение? 3. Каково соотношение между временем и частотой? 4. Синусоида тока имеет эффективное значение 10 ампер. Чему равно ее пиковое значение? 5. Чему равен период синусоиды с частотой 400 герц? 12-3. НЕСИНУСОИДАЛЬНЫЕ КОЛЕБАНИЯ В большинстве случаев форма переменного тока бывает синусоидальной. Однако в электронике используются не только синусоидальные колебания. Колебания, форма которых отличается от синусоиды, называются несинусоидальными периодическими колебаниями. Несинусоидальные колебания генерируются специальными электронными цепями. На рисунках 12-7, 12-8 и 12-9 изображены три основных вида несинусоидальных колебаний. Они могут представлять и ток, и напряжение. На рис. 12-7 изображены прямоугольные колебания, названные так потому, что положительные и отрицательные прямоугольные импульсы чередуются. Это указывает на то, что ток или напряжение 7. 61 Рис. 12-7. Колебание прямоугольной формы. мгновенно достигают максимального значения и остаются такими в течение половины периода. Когда полярность изменяется, ток или напряжение мгновенно достигают противоположного пикового значения и остаются неизменными до конца следующей половины периода. Ширина импульса равна половине периода. Ширина импульса - это отрезок времени, в течение которого напряжение имеет свое пиковое или максимальное значение. Прямоугольное колебание очень полезно как электронный сигнал, так как его характеристики могут быть легко изменены. На рис. 12-8 показан один период колебания треугольной формы. В течение первой половины периода сигнал возрастает по линейному закону от нуля до пикового значения, а затем опять уменьпзается до нуля. В течение второй половины периода сигнал продолжает уменьпзаться по линейному закону в отрицательном направлении до пикового значения, а после этого опять возрастает до нуля. Треугольные колебания используются главным образом как электронные сигналы. Рис. 12-8. Колебание треугольной формы 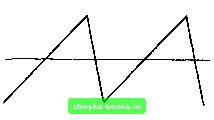 Рис. 12-9. Колебание пилообразной формы. На рис. 12-9 показаны пилообразные колебания. Пилообразное колебание - это частный случай треугольного колебания. Сначала величина напряжения или тока возрастает по линейному закону, а после этого быстро падает до своего отрицательного пикового значения. Участок с положительным наклоном имеет относительно большую длительность и меньший по абсолютной величине угол наклона к оси времени, чем короткий участок. Пилообразные сигналы используются для переключения операций в электронных цепях. В телевизорах и осциллографах они используются для развертки электронного луча по экрану для создания изображения. Импульсные колебания и другие несинусоидальные сигналы могут описываться двумя способами. Один метод рассматривает несинусоидальные сигналы как сумму скачкообразных изменений напряжения, следующих через некоторый интервал времени друг за другом. Второй метод рассматривает сигнал как алгебраическую сумму бесконечного числа синусоид, имеющих различные частоты и амплитуды. Этот метод полезен при расчете усилителей. Если усилитель не может пропустить все синусоидальные частоты, то он искажает сигнал. Несинусоидальные сигналы состоят из колебаний основной частоты и гармоник. Основная частота соответствует скорости повторения сигнала. Гармоники являются синусоидами с более высокими частотами, которые кратны основной частоте. Четные гармоники имеют частоты, которые являются произведениями четных чисел и основной частоты. Нечетные гармоники имеют частоты. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [ 63 ] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] 0.0012 |