нальна его нагрузке, т. е. CJC = Ь/Ь. Чтобы для этого случая воспользоваться круговой диаграммой, необходимо размеры и жесткость выразить через средние величины

Ь = 1/ЬЛ; h=.VhJh; Q==(Qi + Q2)/2.

В случае симметричного расположения амортизаторов система имеет три плоскости симметрии, ZX, XY, YZ, а оси X, Y, Z являются главными центральными осями инерции. При этом коэффициенты ag, ag, а, «26. «з*. «35. «45. «46. «66. 45. р4е. Рбв рэвны нулю И урзвнения (5-2)-(5-7) становятся независимыми друг от друга; из них легко найти все шесть частот:

Из первых трех уравнений этой системы определяются собственные частоты поступательных колебаний вдоль осей X, Y, Z

V ht V т

Из уравнений (5-13)-(5-15) находят частоты вращательных колебаний вокруг осей X, Y, Z

Таким образом, зная параметры амортизированной системы и рассчитав резонансные частоты при выбранных амортизаторах, можно найти величины ускорений, действующих на элементы конструкции, и дать ответ о возможности ее использования в условиях вибрационных нагрузок.

5-4, Расчет механических перегрузок под воздействием ударов

Ударный импульс и его характеристики. Дифференциальное уравнениг вынужденного движения без учета демпфирования. Нахождение максимума ускорения. Оценка защиты РЭА от удара. Расчет смещения амортизированной РЭА под воздействием ударного импульса. Действие линейных перегрузок при вибрации. Влияние демпфирующих устройств амортизаторов

Движение амортизированной системы, вызываемое ударной силой во время ее действия, определяется по законам вынужденных колебаний. После прекращения действия ударной силы движение системы подчиняется закону свободных колебаний. Начальными условиями при этом являются смещение и скорость движения в момент прекращения действия удара.

РЭА и объект, на котором она устанавливается, имеет конечную величину упругости, поэтому действующее ускорение не может передаться на элементы конструкции РЭА мгновенно.

При испытаниях РЭА на стойкость к воздействию ударных нагрузок используют ударный импульс ускорения в виде полуволны синусоиды. Такой импульс характеризуется максимальной величиной ускорения (амплитудой) Л и длительностью действия t. Zi = А sin pt.

Ударный импульс действует только в течение времени времени действия полуволны синусоиды. Период синусоиды Т = 2t, поэтому величина р = зх/и получила название условной частоты импульса. Можно записать:

Возможны и другие формы испытательных ударных импульсов [20]. Дифференциальное уравнение амортизированной массы без учета сил трения будет mz - С (z, - z) = О или

mz + Cz = Czi, (5-16)

где Z - смещение массы т относительно неподвижной системы координат; Zi - смещение основания относительно той же системы.

Продифференцировав дважды (5-16), обозначая z = <з7, z == е7 и подставив выражение для z,, получим + Се7 = СА sin pt.

Для нахождения движения амортизированного блока после окончания действия ударного.импульса воспользуемся операторным методом. Умножим функцию Zi = А sin pt на оператор сдвига е-; эта операция вызовет смещение графика функции на величину % в положительном направлении оси времени. Затем полученную функцию сложим с исходной, получим

Zi = Л (1 -f г-"*/р) sin р . (5-17)

где зх/р = V,.

До удара система была в покое, поэтому е7 (0) = О, е/ (0) = О и уравнение (5-17) можно представить в виде

ms4 + CJ = CA{\+-lp)-, решая относительно if и переходя к оригиналам, получим:

c = -7K2(l-f coscoUsin(co--). (5-18)

Максимум ускорения (рис. 5-11) наступает в момент времени t, = л/2со + tJ2 и зависит от собственной частоты колебаний системы со. Максимальное ускорение в момент времени t, будет

смакс = K2(I+COSC0U-

Коэффициент амортизации удара

Е /21+COS со О cos , (5.19)

Zi макс f> у 1 .iy

где "У = р/со.

Отсюда при -у -> ОО Г] -> 0; при у = I ц = п12; при у = О ц = 0.

График зависимости (5-19) представлен на рис. 5-12. Пользуясь кривой графика, легко найти ускорение на амортизированной РЭА при известной длительности ударного импульса и собственной частоте системы со в направ-ленй-й удара:

0о = Пс7о.с.

где - 55скорение на объекте установки. 124

Если проинтегрировать равенство (5-18) по времени, то можно найти скорость движения и смещение РЭА относительно неподвижной системы отсчета:

=«-[-4r»(«>-"-f)+c.+:J. .

где Ci и Cg - постоянные, определяемые из начальных условий. При t = О, Z = Z = О, поэтому

Ci = cos

Сз- -Sin -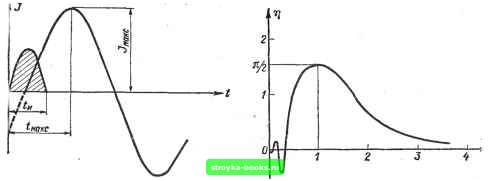

Рис. 5-11. Характер изменения ускорения, действующего на амортизированную РЭА при ударе

Рис. 5-12. Изменение коэффициента амортизации удара Г] в зависимости от отнощения у условной частоты ударного импульса к собственной частоте амортизированной РЭА

Тогда

р2 - СО

-COS-

-cos

«4

Sin-

-cos

Таким образом, зная параметры действующего ударного импульса и собственную частоту амортизированной РЭА, можно найти скорость движения под действием удара и смещение.

С целью упрощения выражений в этих выводах не учитывалось демпфирование системы. При учете демпфирования максимум ц наблюдается при у = 0,75.

Воздействие линейных перегрузок приводит к дополнительным нагрузкам на РЭА. При поступательном движении объекта установки с ускорением а (t) на РЭА массой т, установленную на амортизаторах, будет действовать дополнительная сила Р = та (t). Под действием этой силы амортизаторы прогибаются на величину z. Линейное ускорение а (t) имеет статический характер и поэтому никакими амортизаторами ослаблено быть не может.

Нелинейные амортизаторы, увеличивающие свою жесткость с увеличением статических нагрузок, в условиях постоянных ускорений работают хуже.

При использовании стандартных линейных амортизаторов, имеющих постоянное демпфирование (например, АП, АКСС и т. д.), дифференциальное уравнение движения амортизированной РЭА относительно объекта установки РЭА при постоянной линейной перегрузке будет

7722 + (1 -Ь iym) Cz - ШЯ = О