Параметры оптических линз. Электрические и магнитные поля с осевой симметрией, нли аксиально-симметричные поля, действуют на электронный пучок аналогично действию оптических линз на световой поток. Свойства электронно-оптических линз характеризуются четырьмя кардинальными точками: двумя главными фокусами (f i и f g) и двумя главными плоскостями (h и ftg). Слева от линзы - пространство объек-

А 4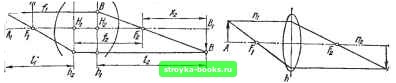

а - б

Рис. 4. Построение изображения в толстой (а) и тонкой (б) оптических линзах

та, или предметное пространство, справа - пространство изображения (рис. 4,0). Если линза тонкая, то главные плоскости сливаются в одну среднюю плоскость h (рис. 4,6).

Расстояния от главных плоскостей до [соответствующих главных фокусов называются фокусными расстояниями: /i= ?\Н, /а= FH. Как следует- из рис. 4,а, линейное увеличение линзы

М = ВВ1АА= xJh= ЛЧ.

(2.3)

Из соотношения (2.3) получаем формулу изображения, отражающую закон Ньютона: х.х.= fj-

Если вместо xi подставить 1- /н вместо х- h- /2 (см- рнс. 4,а), получим формулу линзы j

fi/k+fJk=-

Рис. 5. Ход лучей в тонкой электронной линзе

Для тонкой линзы «1= «2 и соответственно Д= /g-Параметры электронных линз. По аналогии с оптическими линзами параметрами электронных линз являются кардинальные точки, причем для электронной линзы показатели преломления справа и

слева от нее равны соответственно щ = YU (Ь) и = У U (а).

В качестве примера рассмотрим тонкую линзу, для которой раЗ ность потенциалов в области предмета и изображения незначительна. У такой линзы расстояние до предмета и изображения значительно больше ее толщины, т. е. аЬ < 1 (рис. 5). (На рис. 5 точка А является изображением точки А). В тонкой линзе траектория электронов искривляется незначительно (г{а)~г(г)), т. е. электрон практически движется паралле.; ьно оси z.

Фокусное расстояние тонкой электронной линзы с аксиально-симметричным полем определяется из основного уравнения движения

электронов. Проинтегрировав уравнение (2.1) в пределах аЬ действия поля линзы и приняв t/ (а) = U (Ь), получим .

1 1 i \ dz

li l-i 4VVa J f и (г)

Если электронный пучок попадает на участок аЬ линзы слева па-раллельно оси г, т. е, = оо, то величина /j равна фокусному расстоянию линзы /а-

/2 " 4}/"иЩ

dWiz)

- dz.

VU (г)

Аналогично находим 1 и для f, когда луч входит в линзу справа.

Из полученных выражений следует: с ростом потенциала на оси симметрии поля г растет фокусное расстояние линзы / и уменьшается се оптическая сила \lf; оптическая сила линзы увеличивается с росном второй производной от потенциала на оси г (rfi/ {z)ldP), при этом сила, действующая на электрон, направлена в сторону этой оси; фокусное расстояние линзы не зависит от заряда и массы движущейся в ней заряженной частицы.

Аберрации электронных линз. При прохождении электронных пучков через электронные линзы возможны искажения (абберации) изображения на экране, которые могут быть следствием различных причин. В световой и электронной оптике различают следующие виды абберации.

Геометрическая, связанная с нарушением условий параксиаль-иоети движения электронного пучка. Отдельные траектории электронов удалены от оси г и изображение не совпадает с изображением, построенным согласно теории параксиальности траекторий электронов. Разновидностями геометрических абберации являются сферическая абберация, кома, астигматизм, дисторсия.

Хроматическая, связанная с разбросом скоростей движения электронов в пучке. Скорость движения крайних электронов пучка всегда несколько ниже скорости электронов в центре. Поэтому имеет место искажение изображения. Так как оптическая сила линзы зависит от скорости электронов, электронный пучок с различными сксрсстя.чи электронов сойдегся не в одной точке на оси (фокус линзы), а в нескольких.

На искажение изображения может оказывать влияние пространственный чар пучка. Накопление в электронном пучке отрицательно заряженных электронов приводит к образованию расталкиваюш!й лучок силы, что затрудняет сведения его в точку.

Искажения в электронных линзах могут быть также следствием яесоосности сборки линз и прожектора в целом, нестабильности питающих напряжений и др.

8. ТИПЫ ЭЛЕКТРОННЫХ линз

Наиболее широкое практическое применение получили следующее ТИПЫ электронных линз: линза-диафрагма, иммерсионная, одиночная, квадрупольная и иммерсионный объектив. Эти линзы имеют место для

большинства типов электронных прожекторов, так как детали (электроды) прожектора изготовляются круглой формы с осевой симметрией й при включении напряжений на эти электроды вокруг оси г прожек. тора образуется аксиально-симметричное поле, а в пространстве между электродами с разными потенциалами образуются линзы. Если по ходу движения электрона вторая производная от потенциала больше нуля (t/"(z) > 0)> лннза будет фокусировать пучок (собирающая линза), и наоборот, если <У"(г) < О, пучок электронов будет дефокусироваться (рассеивающая линза).

£, jjl)

Рис. 6. Распределение потенциала и ход лучей в линзе-диафрагме (а), иммерсионной (б) и одиночной (е)

Линза-диафрагма. Предположим, что электронный пучок проходит круглую диафрагму вблизи оси г и движется в направлении увеличения потенциала поля (рис. 6,а). При достижении пучком диафрагмы напряженность полн начнет увеличиваться за счет действия электрода с напряжением t/j 200 В. Если потенциал диафрагмы f/д увеличить до 170 В, линза будет иметь уже рассеивающие свойства, т. е. концентрация поля увеличится в отверстии диафрагмы за счет действия собственного потенциала. Так как линзу, образованную диафрагмой. Можно считать- тонкой, оптическая сила такой линзы

Где V{ и {/2-градиента-цот.енциа-4гз.р§ енрдт!ОТпДифрагмы.