запрещенной зоны велика, и, следопательно, для перехода валентных электронов в зону проводимости им нужно сообнщть значительную энергию (не менее 3 эВ). Для полупроводников запрещенная зона относительно невелика (примерно 0,5-3 эВ), и под действием внешних факторов (тепло, свет, электрическое ноле и т. п.) электроны за счет изменения запаса энергии могут перейти нз нормальной зоны в зону проводимости. Электропроводность полупроводников неустойчива и сильно зависит от внешних факторов. Следует помнить, что понятие энергетический уровень или энергетическая зона характеризует толь-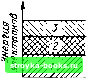

Рис. 1.3. Энергетические диаграммы различных веществ:

а - проводника; б - диэлектрика; в - полупроводника (/ - валентная зона; 2 - запрещенная зона; 3 - зона нронодн-мости).

ко энергетическое состояние электрона, а не геометрическое расположение его в теле.

Свойства электронов достаточно хорошо изучены. Электрон - это электрически заряженная частица, имеющая: отрицательный заряд е = 1,602 10~ Кл; массу nif. =9,109 • 10~ кг; радиус Ге = 2,82

10" м;

удельный заряд

1,759 . 1011

Ни одна другая iacTnna не имеет такого большого значения -,

как .электрон. Это позволяет легко отличать его от других частиц. Электроны обладают следующими основными свойствами:

1) в электрическом поле электроны испытывают воздействие силы и сами могут создавать электрическое поле;

2) электроны, отталкиваются друг от друга;

3) движуииеся электроны образуют электрический ток. Следовательно, подобно электрическому току, проходящему по проводу, поток электронов создает магнитное поле и в поперечном магнитном поле сам испытывает воздействие силы;

4) находясь в движении, электрон обладает кинетической энергией,

равной --, При столкновении э.яектронов с каким-либо телом их

кинетическая энергия превращается в тепловую; при соударении дви-жуиегося электрона с нейтральным атомом кинетическая энергия электрона может быть затрачена на ионизацию атома:

5) благодаря большой величине - электрон обладает высокой по-движностью.

Как уже отмечалось, в соответствии с квантовой теорией электроны, помимо свойств, нрисупщх отдельным материальным частицам (корпускулам), обладают также и волновыми свойствами. Установлено, например, что электронам, как и световым лучам, свойственно явление дифракции, т. е. огибание препятствия, поставлеииого иаих пути. Особенно заметны волновые свойства электронов в пространстве, ли-неЙ!1ые размеры которого сравнимы с размерами электрона.

1.2. РАБОТА ВЫХОДА ЭЛЕКТРОНОВ

Для работы электровакуумных и ионных приборов необходимы свободные электроны, которые надо ввести внутрь баллона. Как их получить? На первый взгляд, ответ не вызывает затруднений - ведь каждое из окружающих нас веществ содержит множество электронов. Задача заключается лишь в том, чтобы «извлечь» их из вещества и ввести в вакуумный или газонаполненный баллон. Но, оказывается, это возможно лишь при выполнении определенных условий. Каких? Об этом и пойдет речь ниже.

При температуре абсолютного нуля (Т = О К) и отсутствии других источников возбуждения электроны в атомах любого вещества занимают уровни с наименьшей энергией. В проводниках, обладающих высокой концентрацией электронов в зоне проводимости, распределение электронов по величинам энергии можно изобразить графиком (рис. 1.4), названным распределением Ферми (по оси абсцисс отложено значение энергии, а по осп ординат-количество электронов). Из графика (кривая }) видно, что при температуре абсолютного нуля пет электронов, обладающих энергией, большей Wp (уровень Ферми). Величина Wp зависит от физических свойств материала и определяется выражением

I 3N Y (1.7)

8m»

где h - постоянная Планка; nie - масса электрона; N -- число свободных электронов в 1 см проводника.

В металлах А 10 10. Поэтому максимальная энергия Uf электронов внутри металла достигает десятков электронвольт. Однако выход электронов за поверхность металла при температуре абсолютного нуля и отсутствии внешних воздействий (освеще1ше новерхностп проводника, бомбардировка пучком электронов и т. и.) не наблюдается. Это объясняется двумя причинами. Во-первых, те немногие электроны, которьк выходят за пределы проводника, теряют большую часть своей энергии и накапливаются на поверхности металла. Между этими электронами и положительными ионами, находящимися внутри металла у его поверхности, образуется электрическое поле, паправлеи-ное от проводника к слою электронов (рнс. 1.5). Совокупность поло-жителы[ых ионов у поверхности металла и электронов, появляющихся над поверхностью, называется двойным электрическим слоем. Действие двойного электрического слоя на электроны, стремящиеся покинуть пределы металла, является 1ормозящим, так как этим

электронам приходится лететь по направлению электрических силовых линий и отдавать свою энергию полю.

Во-вторых, если некоторое количество электронов все же вышло за пределы металла в окружающую среду, то металл будет обратно их притягивать. Объясняется это тем, что металл, лишенный части электронов, заряжается положительно и, следовательно, между ним и вылетевшими электронами возникает электрическое поле, препятствующее выходу новых электронов.

Таким образом, для отрыва от поверхности проводника электроны должны затратить работу против электрических сил, возвращающих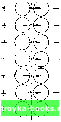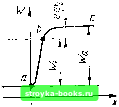

Рис. 1.4. График распределения электронов по величинам энергии в зоне проводимости (распределение Ферми).

Рис. 1.5. Двойной электрический слой на поверхности металла.

/Четалл Вакуум

Рис. 1.6. Энергетическая диаграмма для границы металл - вакуум.

их обратно, т. е. некоторую полную энергию

W, = W-W,. (1.8)

Величина W называется работой выхода. Работа по перемещению электрона из проводника в окружающее пространство равна ироизве-деиню заряда электрона е на пройденную разность потенциалов сро-Поэтому

W, = W,-Wp = erp,. (1.9)

Эта работа измеряется в электронвольтах (эВ).

Диаграмма изменения энергии при переходе электрона из металла в вакуум приведена на рис. 1.6. По оси ординат отложена величина энергии в соответствующих точках пространства, а по оси абсцисс - расстояние от поверхности металла. В целом кривая изображает потенциальный барьер, удерживающий электроны в металле. Участок аЬ соответствует максимальной энергии электрона Wf внутри металла; высота потенциального барьера определяет полную энергию W, которую электрон должен иметь для вылета из металла, разность этих энергий соответствует работе выхода электрона еср-

Величина работы выхода твердых тел зависит от их структуры и является физической характеристикой тела. Чем меньше у данного проводника работа выхода, тем меньшей должна быть затрата энергии для получения свободных электронов вне этого проводника.