в эют момент конденсатор по.чностью разрядится и напряжение на нем упадет до нуля. Далее ток в контуре начнет уменьшаться, что приведет к уменьшению энергии магнитного поля катушки. При эюм по закону Ленца в катушке возникает э. д. с. самоиндукции, которая поддерживает умеиьшаюшийся ток.

Этот ток вновь зарядит конденсатор, но полярность напряжения иа обкладках окажется противоположной по сравнению с предыдущим случаем. В процессе перезарядки конденсатора происходит переход энергии магнитного поля катушкн в энергию электрического поля конденсатора. В тот юмeнт, когда ток упадет до нуля, напряжение на конденсаторе достигнет первоначальной величины. После этого

J- С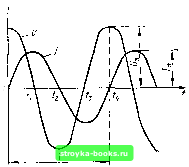

Рис, 15.1. Колебательный контур.

Рнс. 15.2; Графики напряжения и тока в контуре.

конденсатор начнет разряжаться в противоположном направлении и процесс обмена энергией между конденсатором и катушкой будет повторяться.

Характер изменений напряжения на конденсаторе и тока в контуре иллюстрирует рис. 15.2.

Описаиньтй выше процесс разряда конденсатора и возрастания тока разряда показан иа отрезке О - г1. В момент t- напряжение V на конденсаторе равно нулю, а ток / достигает максимального значения /„,. С моме[{та t- ток в контуре уменьшается, но его направление остается неизменным. Конденсатор начинает заряжаться, на его обкладках возникает напряжение с противоположной полярностью (кривая па-пряжения на графике идет ниже оси абсцисс). В момент 4 ток / дос"и-гает нуля, а напряжение на конденсаторе- максимального значения и~. Вся энергия магнитного поля катушки переходит в энергию электрического поля конденсатора. Начиная с момента происходит разряд конденсатора, а ток /, проходящий в противоположном направлении, увеличивается. В момент 1 конденсатор полностью разрядится, а ток достигнет максимального значения. На участке - происходит заряд конденсатора и соответственно уменьшение тока. В момент

восстанавливается исходное состояние и эти?,1 завершается полный цикл колебаний. Далее процесс повторяется.

Таким образом, в контуре происходит периодический колебательный процесс перехода энергии электрического ноля конденсатора в

энергию магнитного поля катушки и наоборот. Такой процесс называют процессом электромагнитных колебаний.

Колебания, происходяш,ие в контуре при отсутствии в нем источника переменной э. д. с, называют свободными колебаниями.

Частоту свободнь[Х колебаний определяют величины L и С контура. В самом деле, если пренебречь потерями энергии в контуре, т. е. считать контур идеальным, то в процессе колебаний энергия электрического поля полиостью переходит в энергию магнитного поля и наоборот. Поэтому можно принять

-7. (15.3)

Для колебательного контура справедливы законы и положения теоргш переменного тока. Так, зависимость между амплитудой тока /,„ и ампл[1тудой напряжения на конденсаторе выражается соотношением

/. = ~ = ЛС, (15.4)

0)пс

где (Од - угловая частота тока в контуре.

Подставив это выражение в равенство (15.3), получим

откуда угловая частота

сй, = --1 (15.5)

Но «о = 2nffj. Следовательно,

где /о - частота свободных (собственных) колебаний контура, Гц; L - индуктивность катушки, Г; С - емкость конденсатора, Ф.

Таким образом, чем больше емкость и индуктивность контура, тем ниже частота его собственных колебаний.

Период свободных колебаний контура определяют по формуле

Го = = 2я ]/LC. (15.7)

Из равенства (15.3) молшо найти амплитудное значение тока в контуре

где р = -- = / - волновое, илн харатеристическое, сопротивление контура.

Нетрудно убедиться, что но своему физическому смыслу вол1[овое сопротивление контура р является индуктивным сопротивлением катушки или емкостным сопротивлением ко}£денсатора для тока свободных колебании fp - WqL = -~\ V w„c j

Процесс свободных колебаний в контуре мог бы продолжаться бесконечно долго, если бы контур состоял только нз емкости и индуктивности. Практически в любом реальном контуре колебания достаточно быстро затухают, так как при каждом переходе энергии из конденсатора в катушку и наоборот часть ее расходуется на активном сопротивлении проводштков, вдиэлектрике конденсатора, а также в результате рассеивания электромаг-ш-1ТИ0Й энергии в окру-жающее пространство.

Графически затухаю-{цие колебания в контуре иллюстрируются рис. 15.3. В зaвиcиюc-ти от соотношения параметров контура L, С и активного сопротивления потерь R колеба1И1я могут затухать с разной скоросгью. Чем больше R, тем быстрее затухают колебания. Можно представить себе такую электрическую цепь, в которой R имеет настолько большую величину, что энергия в цепи расходуется быстрее, чем измен]1тся направление тока в цепи. Такая цепь колебательных свойств ие имеет и ее называют апериодической.

Для оценки скорости затухания колебания используют специальный параметр называемый декрементом затухания. Он показывает, какую часть энергии теряет контур за один полупериод колебаний. Вследствие того, что потери энергии в контуре за полупериод составляют

Рис. 15.3. Затухающие колебания в контуре.

а запасенная в контуре энергия

За-мспив Tq - , получим

(15.8)