15.3. П.\РАЛЛЕЛЫ1ЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР.

РЕЗОНАНС то!гов

Схема подключения генератора к параллельному колебательному контуру показана на рис. 15.6. Учитывая, что потери энергии в конденсаторе обычно невелики, отнесем все потери энергии в контуре к катушке индуктивности, сосредоточив в индуктивной ветви активное сопротивление R.

Рис. 15.6. Параллельный колебательный контур.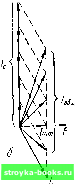

Рис. 15.7. Векторные диаграммы параллельного колебательного контура:

а - при неизменных токах в ве.вях; б- при изменении тоиа □ емкостной ветви

Обе ветви контура находятся под одинаковым напряжением. Ток /общ» идущий от генератора, разветвляется на токн 11 и 1с:

1l =

1с =

= ЕыС.

(15.16) (15.17)

Ток в индуктивной ветви отстает по фазе от напряжения Е на некоторый угол tpL, определяемый по формуле

cos фL

;i5.i8)

Ток в емкостной ветви, наоборот, опережает напряжешзе на 90".

Построив векторную диаграмму для данного случая (рис. 15.7, а), видим, что ток генератора, проходящий в иеразветвлениой части цегщ (/общ на рис. 15.7, а), равен геометрической сумме векторов It и /с; он показан на рис. 15.7, а как диагональ паралеллограмма, построенного на векторах h и 1с-

Очевидно, что вектор тока /общ меньше, чем векторы токов в ветвях Il и 1с. Подбором емкости или индуктивности контура, т. е. соответствующей настройкой контура, можно установить /общ наименьшей величины (рис. 15.7, б). Нетрудно убедиться, что в этом случае ток /общ min совпадает по фазе с приложенным к контуру напряжением Е,

Такое явление в параллельном контуре, при котором ток в нераз-еетвленной части цепи имеет наименьшее значение, а по фазе совпадает с напряжением генератора, называют резонансом пюков.

Как и при резонансе напряжений, условием резонанса токов яв-

ляется равенство o)(,L -, т. е. резонанс тока наблюдается в ла-

раллельном контуре тогда, когда частота генератора равна частоте

собственных колебаний контура L = -т=-

2кУ LC

Рассмотрим основные свойства параллельного контура при резонансе.

Прежде всего очевидно, что в момент резонанса контур оказывает генератору наибольшее и при этом чисто активное по своему характеру сопротивление. Необходимо отметить, что сопротивление параллельного контура при резонансе (ipa) не равно сопротивлению потерь R. Сопротивление /?рез обычно превышает величину R в тьюячи раз. Резонансное соиротивление параллельного контура (Rpos) зависит от величины активного сопротивления R и соотношения величин L и С, т. е. От волнового сопротивления контура. Чем больше R, тем больше энергии расходуется в контуре и поступает в контур от генератора для поддержания незатухающ.их колебаний, т. е. ток

/общтш в неразветвленной цепи должен быть большим. Следовательно,

чем больше R, тем Rpea ~ -7-меньше.

общ min

. Зависимость резонансного сопротивления от волнового сопротивления р можно установить, сравнивая два контура, имеющие одинаковое сопротивление R и настроенные на одинаковую частоту. Предположим, что первый контур образован большой индуктивностью

Ll н малой емкостью (волновое сопротивление = j/ ~--велико), а второй контур образован малой индуктивностью Ц и большой

емкостью (волновое сопротивление рз = /---мало). Вместе

с тем произведения LiC-i и LC для обоих контуров одинаковы и ко-этому, как видно из формулы = -,~г~-~, они настроены на одинаковые резоцаиспые частоты. Очевидно, чго сопротивления емкостной и индуктивной ветвей у второго контура меньше, чем у первого соз <;

<; o)(,L,; -<; - . Поэтому ток во втором контуре больше, чем в

первом. При этом в активном сопротивлении второго контура будет расходоваться больше энергии и, следовательно, от генератора будет поступать больший ток /общтш для поддержания незатухающих колебаний, чем в первом контуре. Таким образом, при неизменном R резонансное сопротивление параллельного контура тем больше, чем

больше отношение т. е. чем больше волновое сопротивление р - 282

Из приведенных соображений становятся понятными следующие расчетные соотношения для определения величины резонансного сопротивления параллельного контура:

где /?рез - резонансное сопротивление контура, Ом: L - индуктивность контура, Г; С - емкость контура, Ф: R - активное сопротивление контура {сопротивление потерь), Ом.

Резонансное сопротивление параллельного контура зависит от добротности контура; чем она выше, тем больше резонансное сопротивление. К этому выводу можно прийти, если в формулу {15.19)

подставить значение = Q;

/?pe3-pQ-{15.20) /1;

Найдем соотношение между величиной тока /общ min при резонансс И всличи-ной тока в контуре (Il = lc}- Вследствие того, что

/общ min "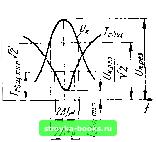

получаем

общ т I и

общ m In

Рис, 15.8. Резонансные параллельного контура.

кривые

Таким образом, .при резонансе в параллельном контуре ток в каждой из его ветвей приблизительно в Q раз превышает ток в неразвет-влгнной части цепи. Поэтому резонанс в параллельном контуре и получил название резонанса токов.

В электронных схемах явление резонанса токов используется очень часто. Практически в большинстве случаев параллельный контур применяют как сопротивление нагрузки в выходной цепи усилительного элемента избирательного усилителя. Сам усилительный элемент в этом случае может рассматриваться как генератор, имеющий определенное {иногда достаточно большое) виутренее сопротивление. Понятно, что э. д. с, которую развивает генератор, распределяется между его внутренним сопротивлением и сопротивлением нагрузки. Для т::го чтобы значительная часть напряжения выделялась на нагрузочном сопротивлении, оно (это сопротивление) должно быть достаточно большой величины. Именно это и обеспечивается контуром при парал-лслы;ом резонансе.

Мзинрательные свойства параллельного контура, как и последо-вательиого, характеризуются резонансными кривыми. На рис. !5-8 показаны графики зависимости напряжевия на контуре (U) и тока