2.5]

ГРАФ ПЕРЕХОДОВ

(&*, ) V {IkJi,) V . V [IkJi) Каждый, член вида llkJZt) содержащийся в обозначении дуги, называется парой вход-выход. Изложенное правило построения графа переходов автомата иллюстрируется рис. 2.1. Это правило устанавливает взаимно однозначное соответствие ме-жду графом переходов и таблицей переходов для одного и того же автомата, так что, зная одно представление, всегда можно получить другое. Для примера на рис. 2.2 изображен граф переходов автомата Л1, построенный по таблице 2.2.

(Ti/ffj (d/o)(n/oNium(Am

(п/Ш

(cf/ffm/mfM/

Ju/O) /ш)1(и/0)(Я/01

Рис. 2.1. Обозначение дуги.

т/1)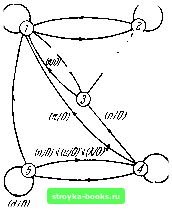

Рис. 2.2. Автомат А\.

По построению графа дуга, направленная из вершины О; к вершине Оу, обозначается входными символами, которые вызывают переход автомата из состояния в Оу, и выходными символами, которые выдаются автоматом при этом переходе. Для детерминированного, без ограничений на входе

«или V -стандартный символ, обозначающий логическую связь

автомата каждый входной сигнал вызывает переход из каждого состояния только в одно другое состояние; следовательно, дуги, выходящие из любой данной вершины, содержат полное число р пар вход-выход, где р - мощность входного алфавита. Непосредственное преимущество графа переходов состоит в том, что он облегчает определение реакции автомата на входную последовательность любой длины. При данном начальном состоянии о автомата М и входной последовательности , „.....Ъ, реакция М легко определяется прослеживанием (в направлении стрелок) непрерывной последовательности / дуг, которая начинается в вершине о,- и k-я дуга которой (A= 1, 2, .. ., /) соответствует паре вход-выход QuJv- Выходная последовательность, которую выдает автомат М при подаче на него входной последовательности , ....., тогда будет

С»,. Xv, •. Ц; состояние, в которое при этом переходит М, определяется по обозначению вершины, в которой заканчивается последовательность из / дуг. Например, реакция автомата А\ на входную последовательность nunXXdn при начальном состоянии 3 легко определяется по рис. 2.2 и будет 0000001. Последовательность состояний при этом будет 1, 3, 4, 4. 4, 5 и 1.

Роль графа переходов в теории конечных автоматов подобна роли, которую играет графическое изображение схемы в теории электрических цепей. Граф переходов преобразует абстрактную модель в физическое изображение, усиливающее интуицию исследователя, и дает возможность ему «отчетливо представить» различные процессы и свойства, которые без такого изображения остались бы рядом сухих математических фактов. Как и в теории цепей, граф переходов удобно рассматривать как модель саму по себе, а символы, используемые в графе, - как абстрактные компоненты модели. Поэтому часто в дальнейшем мы будем граф, представляющий автомат М, называть «автоматом Ж», вершину, представляющую состояние О;, - «состоянием О;» и, наоборот, отождествлять абстрактные понятия с их геометрическими представлениями, имеющимися в графе переходов.

Понятие изоморфизма конечных автоматов, введенное в § 2.4, в терминах графов переходов допускает очень

простую интерпретацию: автоматы изоморфны один другому, если они имеют одинаковые графы, отличающиеся, быть может, только обозначением вершин. Таким образом, для того чтобы автомат М заменить изоморфным ему автоматом, надо просто изменить обозначение одной или нескольких вершин. Аналогично, чтобы получить семейство перестановок автомата М, достаточно переставить обозначения вершин всеми возможными способами.

2.6. Классификация состояний и подавтоматов

Дуга относительно данного состояния, например, О;, может быть заходящей в О;, если она направлена к из другого состояния, или исходящей из о,-, если она направлена от к другому состоянию, или петлей, если она выходит из Ol и входит в О;. На рис. 2.3 показаны эти тр1 шу\ типа дуг.

Состояние, в котором от-сутствуют заходящие и (или)

исходящие дуги, может быть

одним из следующих типов:

(1) преходящее состояние - состояние, которое не имеет заходящих дуг, но имеет, по крайней мере, одну исходящую дугу; из этого состояния может быть осуществлен переход, по крайней мере, в одно другое состояние, но после выхода из этого состояния, в него нельзя попасть ни из какого друго;-о; (2) тупиковое состояние - состояние, которое не содержит исходящих дуг, но содержит, по крайней мере, одну заходящую дугу; в такое состояние может быть осуществлен переход, по крайней мере, из одного другого состояния, но после перехода в это состояние из него нельзя осуществить переход ни в одно другое состояние; (3) изолированное состояние-состояние, которое не содержит ни заходящих, ни исходящих дуг; из такого состояния нельзя перейти ни в какое другое и в него нельзя попасть ни из какого другого состояния. На рис. 2.4 приведен автомат А2, в котором состояния 1 и 5 являются преходящими, состояния 2 и 4-тупиковыми, а состояние 6 - изолированным.