Любое разбиение множества состояний автомата на два или большее число подмножеств может быть, очевидно, выполнено путем заключения представленных графом переходов

(л/У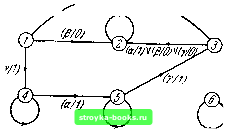

гис. 2.4. Автомат А2.

состояний каждого подмножества в отдельный «прямоугольник», рассматриваемый как подавтомат. На рис. 2.5 и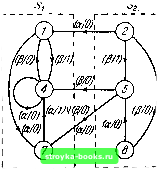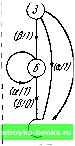

gy(am(fi/V

Рис. 2.5. Автомат ЛЗ.

в таблице 2.4 представлен автомат ЛЗ, множество состояний которого S={1, 2, 3, 4, 5, 6, 7, 8, 9) разделено на подмножества S,= {1,4. 7). S2={2. 5, 8) и 5з={3, 6, 9); три подавтомата, изображенные в виде прямоугольников, обозначены на рисунке символами Sj, и S3.

Рассматривая каждый подавтомат как одно «сверхсостояние», преходящий, тупиковый или изолированный подавто-

маты могут быть определены точно так же, как преходящее, тупиковое и изолированное состояние с заменой слова «состояние» на слово «подавтомат», именно: (1) преходящий подавтомат можно перевести, по крайней мере, в один другой подавтомат, но он не может быть достигнут после того, как оставлен; (2) тупиковый подавтомат может быть достигнут, по крайней мере, из одного другого подавтомата, но не может быть покинут после того, как он достигнут; (3) изолированный подавтомат не может быть достигнут ни из одного другого подавтомата и не может привести ни в какой другой подавтомат. Граф переходов часто позволяет визуально определить, составляет ли определенное подмножество множества состояний преходящий, тупиковый или изолированный подавтомат, и, следовательно, сделать заключение об относительной доступности этого подмножества. Например, из рис. 2.5 можно легко заключить, что 5) - тупиковый подавтомат, Sj - преходящий подавтомат, а S3 - изолированный подавтомат.

Пусть Gii{Si) обозначает множество всех состояний автомата М, в которые можно попасть из любых состояний множества 5, = {о;, о,-.....0; при подаче на вход последовательности длины k или меньше. В частности, Gq(5) = S,-. Множество Gi(S;) есть объединение и всех состояний, указанных в строках о,, ai, о, подтаблицы s таблицы переходов М. С другой стороны, Gi(5;) может быть определено путем просмотра графа переходов

.Таблица 2.4

Таблица переходов автомата A3

Это значит, что алгоритм 2.1 требует не более чем п - г итераций пункта 2. Таблица 2.5 иллюстрирует применение алгоритма к автомату ЛЗ, изображенному на рис. 2.5, для = {5, 6), который дает G(5, 6)={1, 3, 4, 5. 6. 7. 9).

Если Si состоит из одного состояния о,-, то G (о) называется ai-достижимым множеством и представляет собой множество всех состояний, в которые можно попасть из состояния о,-.

Теорема 2.2. Пусть и Oj - два состояния в автомате с п состояниями. Если Oj вообще достижимо из о,-, то оно достижимо при подаче входной последовательности длиной не более п-1.

автомата М. Если задано G;j i(S), Al, то G(Si) может быть определено из соотношения

G,(S;) = G,(G, i(S,)). (2.7)

Если G,{Si) = G, ,iSi), то G;„(S) = G;, i(S) для всех неотрицательных целых и; следовательно, (S;) составляет множество всех состояний, в которые можно попасть из S, если на вход подавать последовательности любой длины. Определение этого множества, обозначаемого просто G(5;). может быть теперь описано при помощи следующего алгоритма.

Алгоритм 2.1. Дано S; найти G{Si). (1) Пусть Go(5;) = S. Полагаем k=l. (2) Определяем G{S,) = = G,(G, ,(5;)). (3) (а) Если G, (S) G, , (S). увеличиваем А на 1 и возвращаемся к (2). (б) Если G; (S) = G; i (S), то G,{Si) = G{S,).

Если G{Si) Ф G i(Si), то G(Si) должно содержать, по крайней мере, на один элемент больше, чем G -{Si). Так как мощность G/iSi) не может превышать общее число п

состояний автомата Ж, то G;j(S,) Таблица 2.5 должно равняться G i{Si) для Алгоритм 2.1 А < л -г-f-1. где г- мощность

для автомата A3 множества Следовательно,

и для 5.= {5, 6, G(S,)=G (S,). (2.8)