3.2) ЭКВИВАЛЕНТНОСТЬ СОСТОЯНИЙ 77

Некоторые из этих случаев описываются с помощью следующих трех лемм.

Лемма 3.1. Пусть Oi и Oj-состояния автомата М. Если строки Oi и Oj в подтаблице г, автомата М различаются, то афОу

Доказательство. Очевидно, существует по крайней мере один входной символ, при приложении которого к Жа; и к M\(yj, на выходе М получаются различные выходные символы. Следовательно, по определению 3.1 Oi=ji=aj.

Лемма 3.2. Пусть и Oj - состояния автомата М. Если строки и Oj в полной таблице переходов автомата М одинаковы, то ai = aj.

Доказательство. При приложении к Жа, и к M\aj любого входного символа выходные символы и следующие состояния в обоих случаях будут одинаковы. Поскольку Ж0; и M\aj переходят в одно и то же состояние, их реакции на все подпоследовательности входных сигналов должны совпадать. Следовательно, по определению 3.1 а; = ау.

Лемма 3.3. Пусть и оj-состояния автомата М. Если строки и Оу полной таблицы переходов автомата М становятся одинаковыми при замене каждого обозначения на Oj {или наоборот), то ai = aj.

Доказательство. При приложении любого входного символа к Жа; и к M\aj выходные символы одинаковы в двух случаях: либо Жа и M\Oj переходят в одно и то же состояние, либо в состояния О; и Oj (не обязательно

соответственно). Если следующее состояние одно и то же, то реакции автомата на входные подпоследовательности будут совпадать. Если следующими состояниями являются и Оу, то восстановится исходная ситуация, и приведенные выше соображения можно будет повторить, чтобы показать, что следующие выходные символы одинаковы в обоих случаях. Затем, по индукции, получим, что реакции при О; и Oj на любую входную последовательность будут одинаковыми, откуда следует, что ai = Oj.

Пары строк, обладающие свойством, приведенным в лемме 3.1, называются явно различимыми, а состояния, стоящие в основном столбце в этих строках. - явно разли чимыми состояниями. Пары строк, обладающие свойствами,

указанными в леммах 3.2 и 3.3, называются явно эквивалентными, а состояния, стоящие в основном столбце в этих строках,-явно эквивалентными состояниями. Таким образом, имеем:

Теорема 3.1. Если состояния О; и Oj явно различимы, то OlФOj, а если состояния О; и Oj явно эквивалентны, то 0 = 0J.

Следует отметить, что утверждение, обратное теореме 3.1, несправедливо, т. е. не каждая пара различимых состояний является явно различимой и не каждая пара эквивалентных состояний явно эквивалентной. Используя определения, введенные в § 2.3, можно заключить, что в явно минимальном

(y/7J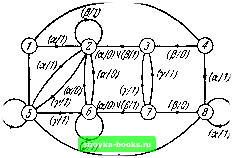

Рис. 3.1. Автомат Л6.

автомате все пары состояний различимы, а в явно сократимом автомате имеется по крайней мере одна пара эквивалентных состояний.

Для иллюстрации лемм 3.1-3.3 рассмотрим автомат Л6, представленный графом переходов, изображенным на рис. 3.1, и таблицей переходов 3.1.

Из таблицы переходов видно, что строки 1 и 5 одинаковы, а строки 2 и 6 становятся одинаковыми, если каждую цифру 2 заменить на цифру 6 (или каждую цифру 6 заменить на цифру 2). Следовательно, состояния в парах {1,5} и {2, 6) являются эквивалентными. Рассмотрение подтаб-

3.3]

-ЭКВИВАЛЕНТНОСТЬ

Автомат i46

Таблица 3.1

лицы показывает также, что ни одно состояние из множества {1, 4, 5, 8} не может быть эквивалентным какому-либо состоянию из множества {2, 3, 6, 7}.

3.3. А-эквивалентность

Для дальнейших обсуждений полезно ввести понятие «-эквивалентности».

Определение 3.2. Состояние О; автомата Ж; и состояние Oj автомата М2 называются k-эквивалентными, если при приложении к Жа и к Ж20у входной последовательности длины k они вырабатывают одинаковые выходные последовательности. Если О; и Oj не являются -эквивалентными, то они называются k-различимыми. Обозначения и Ж2 могут относиться к одному и тому же автомату.

Таким образом, и являются й-эквивалентными тогда и только тогда, когда, прикладывая входные последовательности длины k и наблюдая сигналы на внешних выходах, невозможно отличить автомат Ж; в состоянии О; от автомата Ж2 в состоянии Oj. Состояния О; и Oj являются &-раз-личимыми тогда и только тогда, когда имеется хотя бы одна входная последовательность длины к, которая при приложении к Ж1а; и M2\0j вырабатывает разные выходные последовательности. Два 1-различимых состояния, согласно определению, данному в § 3.2, являются явно различимыми.

На основании определения 3.2 легко показать, что -эквивалентные состояния обладают свойствами рефлексий-