ности, симметричности и транзитивности. Следовательно, -эквивалентность можно трактовать как обычное отношение эквивалентности, которое непосредственно применимо к множествам состояний любой мощности. С другой стороны, -различимость не обладает свойствами рефлексивности и транзитивности, и, следовательно, это понятие применимо только к парам состояний.

Лемма 3.4. (а) Если два состояния являются k-эквива-лентними, то они являются и 1-эквивалентными для каждого lk. (б) Если два состояния являются k-различимыми, то они являются и (-различимыми для каждого lk.

Доказательство, (а) Пусть О; и Oj являются -эквивалентными, но различимыми при некоторой входной последовательности, скажем длины lk. Тогда О; и Oj должны

быть различимы при входной последовательности где представляет собой любую входную последователь-

ность длины k - /. Следовательно, О; и Оу являются k-раз-

личимыми, что противоречит условию, (б) Пусть О; и Оу являются различимыми, но /-эквивалентными для некоторого 1" k. Однако, согласно (а), если О; и Оу являются -эквивалентными, они должны быть -эквивалентными для каждого kl. Полученное противоречие доказывает справедливость утверждения (б).

Состояние, в которое переходит состояние О;, при подаче входной последовательности длины k называется k-м преемником О;, по отношению к этой последовательности. Нулевым преемником состояния является само состояние.

Теорема 3.2. Если состояния О; и Oj являются k-эквивалентными и если их k-e преемники по отношению к любой входной последовательности длины k являются эквивалентными, то ai = Oj.

Доказательство. Если О; и Оу являются -эквивалент-

ными, то, согласно лемме 3.4, они вырабатывают одинаковые реакции при всех входных последовательностях длины k или менее. Если их k-t преемники по отношению к любой входной последовательности длины k являются эквивалентными, то они вырабатывают одинаковые реакции при всех рходных последовательностях, которые следуют за первыми k

3.31

ft ЭКВИВАЛЕНТНОСТЬ

символами. Следовательно, О; и Оу вырабатывают одинаковые выходы при входных последовательностях любой длины, откуда следует, что ai=aj.

Теорема 3.3. Если состояния Oi и Oj являются эквивалентными, то их k-e преемники по отношению к любой входной последовательности длины k и для любого k являются эквивалентными.

Доказательство. Пусть о\ и а, являются &-ми преемниками состояний О; и Оу соответственно по отношению к произвольной входной последовательности Если o\=hoj, то имеется последовательность, скажем для которой и о, вырабатывают различные реакции. Следовательно, реакции для О; и Оу на ki должны быть разными; это противоречит допущению, что а; = ау.

Входную последовательность, подаваемую на Ali0; и AlglOy, можно сравнить с двумя путями, начинающимися состояниями о,- и Оу на графе переходов для автоматов и М2 соответственно. Теорема 3.3 означает, что если два

I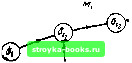

Рис. 3.2. Пути в автоматах М, и AI2 при(Т;=СТу.

начальных состояния на этих путях эквивалентны, то каждые два соответствующих состояния на этих путях (т. е. состояния, в которые переходят автоматы из начальных состояний после прохождения одного и того же числа дуг) являются также эквивалентными. Это положение иллюстрируется рис. 3.2, где показанные пути являются путями, которые

проходят Ml и М2, при приложении некоторой входной последовательности к УИО; и к yMjIoy. Если и Оу являются эквивалентными, то k-e преемники ai и Oj должны быть эквивалентны для всех k.

Изложенные результаты могут быть использованы во многих случаях для установления эквивалентности состояний, когда эквивалентность других состояний уже установлена. Пусть, например, известно, что пары состояний {1, 5) и {3, 7} автомата Л6, изображенного на рис. 3.1, являются эквивалентными. Тогда пара {4, 8} должна быть также парой эквивалентных состояний вследствие того, что 4 и 8 являются 1-эквивалентными, а их первыми преемниками являются пары {1,5) и {3, 7). Если известно, что состояния в паре 4, 8 эквивалентны, то состояния в парах {1,5), {2, 6) и 3, 7 должны быть также эквивалентными, поскольку они образуют пары соответствующих состояний на путях, начинающихся состояниями 4 и 8.

3.4. -эквивалентные разбиения

Для целей, которые станут ясными из следующих параграфов, представляет интерес деление или «разбиение» состояний автомата на классы по следующим правилам: (1) все состояния, принадлежащие к одному классу, должны быть -эквивалентными; (2) все состояния, принадлежащие к разным классам, должны быть -различимыми. Такое разбиение называется k-эквивалентным разбиением автомата и обозначается Я. Классы Р,1 называются классами k-эквива-лентности и обозначаются S*,, 2, S, и т. д. Состояния, принадлежащие к одному и тому же классу, называются смежными состояниями; состояния, принадлежащие к разным классам, называются разобщенными состояниями.

Рис. 3.3 и таблица 3.2 представляют автомат А7. Для этого автомата 2-эквивалентное разбиение имеет вид

Р: 221 = {1, 3, 5, 7, 8),

222 = {2. 4, 6), (3.1)

223= (9)...

Легко проверить по графу переходов автомата А7, что смежные состояния в Р, заданные выражениями (3.1),