с точки зрения анализа, так и с точки зрения синтеза удобно переменные, которые характеризуют систему, различать следующим образом: (1) входные переменные, которые представляют собой воздействия, генерируемые другой системой (не подлежащей исследованию), и которые влияют на поведение исследуемой системы; (2) выходные переменные (реакции), представляющие собой те величины, характеризующие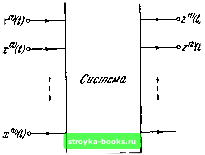

Рис. 1.1. Представление системы в виде «черного ящика».

поведение данной системы, которые интересуют исследователя; (3) промежуточные переменные - те величины, которые не являются ни входными, ни выходными переменными.

Схематично система может быть изображена «черным ящиком» с конечным числом внешних полюсов, доступных для исследователя. Входные полюсы соответствуют входным переменным и снабжаются стрелками, направленными внутрь ящика. Выходные полюсы соответствуют выходным переменным и снабжены стрелками, направленными от ящика. Предполагается, что промежуточные переменные, не представляющие непосредственного интереса, сосредоточены внутри ящика. Входные и выходные переменные и ящик, не имеют какого-либо физического смысла, они просто служат для наглядного представления тех переменных системы, которые имеют отношение к решению данной задачи.

Рис. 1.1 иллюстрирует представление системы в виде черного ящика в том случае, когда она имеет и входных

1.31 ДИСКРЕТНОСТЬ ВРЕМЕНИ 15

И W ВЫХОДНЫХ переменных, причем предполагается, что все

переменные зависят от времени. Символ дг* (i), 4-1,2.....и.

сбэзначает входные переменные, а символ z\t), J =\, 2,... .... W, - выходные переменные.

1.3. Дискретность времени

Предполагается, что любая система, представимая основной моделью с конечным числом состояний, следующим образом управляется некоторым независимым синхронизирующим источником. Все переменные системы измеряются не непрерывно, а только в дискретные моменты времени, в которые подается синхронизирующий сигнал от источника синхронизирующих сигналов. Эти моменты времени называются тактовыми моментами, причем v-й тактовый момент будем обозначать через (v=l,2, ...). Далее предполагается, что поведение системы в любой момент времени не зависит от интервала времени между и Таким образом, фактически независимой величиной, относительно которой определяется каждая переменная системы, является не время, а порядковые номера, связанные с тактовыми моментами. Таким образом, любая переменная системы v(t) может быть записана в виде г», что обозначает значение величины v в v-й тактовый момент.

Следует заметить, что вышеизложенные предположения совсем не означают, что интервалы между соседними синхронизирующими сигналами одинаковы, а переменные системы внутри интервалов изменяются по какому-либо определенному закону (скажем, остаются постоянными). Эти предположения означают только следующее: какой бы ни был интервал времени между синхронизирующими сигналами и какие бы ни были изменения системы внутри этого интервала, значения переменных в v-й тактовый момент зависят только от номера v и не зависят от текущего значения времени

Система, удовлетворяющая изложенным предположениям относительно дискретности во времени, называется синхронной. Асинхронные системы, не удовлетворяющие этим предположениям, в книге не рассматриваются. На практике многие асинхронные системы могут для целей анализа рассматриваться как синхронные. В качестве примера рассмотрим систему, состоящую из ключа и лампы, которую он включает и

отключает. Входной переменной является положение ключа (включен или отключен), а выходной переменной - состояние лампы (горит или не горит). Источником синхронизирующих сигналов в этом случае является оператор, включающий и отключающий ключ, а синхронизирующим сигналом - поворот ключа. В тех случаях, когда можно считать, что значение каждой переменной в v-й тактовый момент (т. е. когда ключ нажат в v-й раз) не зависит от интервалов между моментами синхронизации (т. е. между одним нажатием ключа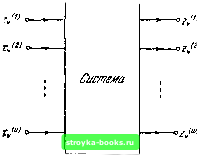

Рис. 1.2. Представление системы в виде «черного ящика» с учетом предположения о дискретности времени.

и следующим), описываемая система может рассматриваться как синхронная. Однако, строго говоря, система является асинхронной, так как работа реальных ключей и ламп зависит от интервала между двумя последовательными включениями, так как если частота переключения становится слишком высокой, то уже не может быть уверенности, например, в том, что свет имеется всегда, когда включен ключ. Тем не менее, когда известно, что частота переключения достаточно низкая (это знание может быть основано на заданных характеристиках синхронизирующего источника), допустимо рассматривать систему как синхронную. Можно отметить, что анализ большинства цифровых вычислительных машин, встречающихся на практике, может быть соответствующим образом проведен в предположении, что эти машины представляют собой синхронные системы.