
 |
|
Главная Кибернетика [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [ 32 ] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] случае, если они одинаковы во всех строках. Разбиение столбцов может быть выполнено вручную даже для большого числа Л/, при этом сразу получается эквивалентное разбиение автоматов без составления перечня всех пар эквивалентных автоматов. Таблица 3.11 Таблица эквивалентности для автомата Д (М, М,М) Класс Автомат 21. 22. В клетках проставляются О или 1 Для иллюстрации, на рис. 3.8 приведены автоматы ЛИ, Л12, Л13 и Л14, объединенные в один расщепляемый автомат Д(Л11, Л12, Л13 и Л14). Таблица 3.12 Автомат Д (Д11, >112, Л13, АН)
Таблица переходов для этого расщепляемого автомата представлена в таблице 3.12. Применение любого из методов эквивалентного разбиения, описанных в §§ 3.6-3.8, показывает. 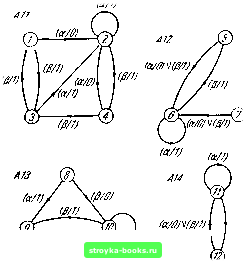 ШЛт (а/7) Рис. 3.8. Автомат Д (11, AV1, А\Ъ, АЩ. что для Д(Л11, Л12, Л13, Л14) классами эквивалентности являются {1, 4, 5. 7, 9, 12), {2, 3, 6, 10, 11) и (8). Таблица 3.13 представляет собой таблицу эквивалентности для Д(Л11, Л12, Л13, Л14), которая показывает, что Таблица 3.13 Таблица эквивалеитиости для Д (ЛИ, AVI, 413, АЩ
au) = ij и fsib, а;) = о;. (3.15) Заметим, что если при приложении ; к Ж в определенном состоянии из 2ц вырабатывается выходной символ t,j, то при приложении li в любом состоянии из 2„ также вырабатывается выходной символ Аналогично, если при приложении li к М в некотором состоянии из 2„ М переходит в состояние, принадлежащее 2,, то при приложении ; в любом состоянии из 2ц М переходит в состояние, принадлежащее 2j,. Таким образом, при построении М по условию (3.15) не возникает никакой неопределенности вследствие того, что о<" является произвольным состоянием, принадлежащим классу 2„, и что о<" является произвольным состоянием, принадлежащим классу 2,. эквивалентным разбиением автоматов для множества автоматов {ЛИ. Л12, Л13, Л14} является {ЛИ, Л12, Л14} и {Л13}. Заметим, что в процессе эквивалентного разбиения автоматов мы получаем также обычное эквивалентное разбиение каждого автомата из заданного множества. Например, эквивалентное разбиение Д(ЛИ, Л12, Л13, Л14), как видно из таблицы 3.13, показывает, что эквивалентное разбиение ЛИ есть {1, 4} и {2, 3}, эквивалентное разбиение Л12 - {5, 7} и {6}, эквивалентное разбиение Л13-{8}, {9} и {10} и эквивалентное разбиение Л14 - {11} и {12}. 3.11. Минимальная форма Пусть М - автомат с п эквивалентными классами, обозначенными 2j, Sj, 2-, и пусть о* представляет собой какое-нибудь состояние в 2;. Минимальная форма автомата М, обозначаемая через М, представляет собой автомат с п состояниями, образующими множество {о, о.....о}. Минимальный автомат строится из М следующим образом. Обозначим характеристические функции автомата М через Д и а автомата М через и тогда, если [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [ 32 ] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] 0.0022 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||