(3.16)

3.12. Свойства минимальной формы

В дальнейшем будем говорить, что автомат меньше или больше М2 в зависимости от того, имеет соответственно меньшее или большее число состояний по сравнению с Mj.

Теорема 3.6. Если М является минимальной формой автомата М, то: (а) М является единственной минимальной формой с точностью до изоморфизмаУ, (б) М=М; (в) никакие два состояния в М не являются эквивалентными; (г) не существует автомата, эквивалентного М и меньшего, чем М.

Доказательство, (а) По лемме 3.5 является единственным для любого /г1 и, следовательно, P„ i = P является единственным. Так как при определенном Р построение Ж из Ж является единственным, не учитывая обозначения, то Ж является единственным с точностью до изоморфизма, (б) Рассмотрим какую-нибудь входную последовательность E/jE/j ••• Ег> приложенную к Жо*". Пусть соответствующая последовательность состояний будет о<", а"\ ..., a"i и соответствующая выходная последовательность будет C/jC/j . • • C/j- Теперь пусть та же входная последовательность приложена к М\а. По условию (3.15),

на основании которого строится Ж по Ж, соответствующая последовательность состояний должна быть о , о , . . ., о

и соответствующая выходная последовательность должна

) То есть с точностью до обозначения состояний.

построении таблицы переходов

3.12] СВОЙСТВА МИНИМАЛЬНОЙ ФОРМЫ Щ

быть .. . t,j. Поскольку в приведенных рассуждениях

I и и являются произвольными, то, следовательно, любое состояние уИ, принадлежащее классу эквивалентности 2„, является эквивалентным состоянию Оц автомата М. Таким образом, для каждого состояния М мы находим эквивалентное состояние М и для каждого состояния М находим эквивалентное состояние М, что означает, что М= М. (в) Пусть Оц и Oj, являются двумя любыми состояниями М{иф V).

Из доказательства части (б) следует, что о„ эквивалентно состояниям М, принадлежащим классу эквивалентности S„, а 0 эквивалентно состояниям М, принадлежащим классу эквивалентности 2,. Так как ни одно состояние-из класса 2„ не эквивалентно никакому состоянию из класса S,, то состояния 0 и 0 автомата М должны быть различимыми, (г) Предположим, что имеется автомат М, эквивалентный М и меньший М. Так как Ж = Л1 и М= М, то это значит, что М= М и что каждое состояние М является эквивалентным некоторому состоянию М. Так как М больше, чем М, то имеются, по крайней мере, два состояния М, которые эквивалентны одному и тому же состоянию М и, следовательно, эквивалентны друг другу. Однако, согласно части (в) теоремы, это невозможно, что доказывает от противного тот факт, что не существует автомата, эквивалентного М, и меньшего, чем М.

Автомат, который является своей минимальной формой и потому не имеет эквивалентного себе меньшего автомата, называется минимальным автоматом. Автомат, имеющий п состояний и п классов эквивалентности, в котором, следовательно, все пары состояний различимы, является минимальным автоматом. Из теоремы 3.6 следует, что если задан какой-либо автомат М, то мы можем найти минимальный автомат М, эквивалентный М и являющийся единственным с точностью до изоморфизма. Этот вывод является исключительно важным, поскольку он говорит нам, что каждый автомат имеет некоторое «каноническое» представление, независящее от способа задания исходного автомата. Действительно в общем случав существует ряд способов,

которыми автомат может быть описан (особенно если это сделано устно), и оказывается, что все это многообразие описаний может быть, в конце концов, сведено к некоторому стандартному представлению. Более того, из сделанного вывода следует, что стандартное представление является наиболее компактным в смысле числа используемых состояний. Если вследствие недостатка опыта или изобретательности у исследователя начальное представление получается сильно избыточным, то имеется прямой способ уменьшить

избыточность до предела и

Ш/ffJ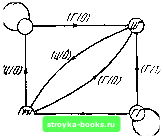

пред-

(r/rj

Рис. 3.10. Автомат Л15.

получить минимальное ставление.

Чтобы проиллюстрировать сказанное, рассмотрим следующую игру; монета подбрасывается многократно; очко засчитывается при v-m подбрасывании, если при (v-2)-м, (v-1)-м и v-m подбрасывании выпадают соответственно: цифра, герб, герб или герб, герб, герб; в других случаях очко не засчитывается. Обозначив «герб» буквой «Г», а «цифру»-буквой «Ц», «очко» - «1», а «отсутствие очка» - «О», мы можем выбрать следующие входной алфавит, выходной алфавит и множество состояний:

={Г, Ц}, Z={0, 1),

5={ЦЦ. ЦГ, ГЦ, ГГ},

где указанные четыре состояния отождествляются со всеми возможными исходами при (v - 2)-м и (v-1)-м подбрасывании. Граф переходов автомата Л15, соответствующего этому описанию игры, показан на рис. 3.10. Однако более компактное представление получается, если заметить, что счет очков при v-m подбрасывании не зависит на самом деле от (v - 2)-го исхода (хотя это может быть замаскировано устным описанием игры). Тогда мы можем выбрать следующие входной и выходной алфавиты и множество