
 |
|
Главная Кибернетика [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [ 36 ] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] В Л63 нет явно эквивалентных состояний, сокращение путем объединения в том виде, в каком оно выполнялось выше, должно на этом закончиться. Оказывается, что полученный сокращенный автомат Л63 является в то же время минимальной формой Л6. Граф переходов Л6з=Л6 показан на рис. 3.12. Следует подчеркнуть, что, поскольку не всякие два эквивалентных состояния являются явно эквивалентными, описанная процедура сокращения не всегда дает минимальный автомат. После того как методом последовательного объединения получен наименьший автомат, следует применять стандартную методику эквивалентного разбиения, чтобы получить минимальную форму автомата или чтобы удостовериться в том, что дальнейшее сокращение невозможно. 3.14. Класс минимальных автоматов Используя определения, введенные в § 2.3, в качестве следствия теоремы 3.1 и определения эквивалентности автоматов получаем: Лемма 3.12. Явно минимальный (п, р, д)-автомат должен быть минимальным. Явно сократимый (п, р, q)-автомат не может быть минимальным. Дополнительно теперь докажем следующие леммы. Лемма 3.13. Мощность семейства перестановок минимального («, р, q)-aemeMama равна п\ Доказательство. Пусть М - минимальный («, р, q)-автомат и пусть - автомат, полученный из М перестановкой обозначений его состояний. Предположим, что перестановка, с помощью которой М2 получен из Ж,, включает в себя замену обозначения состояния из М на «Оу» (У Ф 1). Если Ml и М2 имеют одинаковые таблицы переходов, то реакции Mi\Oj и М2\Oj на любую входную последовательность должны быть одинаковыми и, следовательно, реакции Ml I Оу и Ml I О; на любую входную последовательность также должны быть одинаковыми. Это означает, что состояния О; и Оу в Ml эквивалентны и, следовательно. Mi не является минимальным автоматом. Из полученного противоречия следует, что различные перестановки должны давать 3.14] КЛАСС МИНИМАЛЬНЫХ АВТОМАТОВ 117 в результате различные таблицы переходов. Число различных перестановок равно «!. Лемма доказана. Лемма 3.14. Мощность N„pg класса минимальных («, р, д)-автоматов, таких, среди которых нет двух изоморфных друг другу автоматов, определяется выражением п- 1 п,р,<-Л1(дпГ-г]. (3.17) Доказательство. Пусть число («, р, 9)-автоматов, не являющихся явно сократимыми, равно N„, р, и пусть число минимальных («, р, 9)-автоматов, изоморфных или неизоморфных друг другу, равно N„ . Тогда, согласно лемме 3.12, N <N" . (3.18) Согласно лемме 3.13, Л =n\N (3.19) п, p,q п, p,q • A/„ p , = i}v;,,,<<,,,. (3.20) Используя уравнение (2.3) для определения ы"п, р, q, получаем доказательство леммы. Поскольку два минимальных неизоморфных автомата должны быть различимы, то р, представляет собой также число минимальных («, р, 9)-автоматов, среди которых нет ни одной пары эквивалентных автоматов. Это число должно включать в себя число Nj,p,q явно минимальных («, р, q)-автоматов, среди которых нет ни одной пары изоморфных автоматов. Используя теорему 2.1 для определения Nnlq получаем: Теорема 3.7. Мощность Nn,p,q класса минимальных (п, р, д)-автоматов, среди которых нет ни одной пары эквивалентных автоматов, определяется выражением iП - п,л , < 7ГГ П - (3-21) г-о г=0 Например, общее число минимальных (2,2,2)-автоматов, среди которых нет эквивалентных, заключено между 96 и 120. Задачи 3.1. Покажите, что если а; = ау, а oj Ф о/,, то а; Ф О/;. 3.2. Используя симметричность графа переходов, показанного на рис. 3 3.1, покажите, что а, =02, 03 = 04 и 05 = 0,5. (а/У 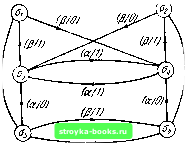 (fi/V Рис. 3 3.1. (а/1, 3.3. В подтаблице автомата М. все строки одинаковы. Покажите, что М. представляет собой тривиальный автомат. 3.4. Покажите, что если /-я и у-я строки матрицы \М\ одинаковы, то состояния О; и Оу автомата М являются эквивалентными. 3.5. Состояния О/ и оу являются Неэквивалентными, а их Ai-e преемники по отношению к любой входной последовательности длины являются *2-эквивалентными. Покажите, что если *i -(- *2 > >/г -1, то 0( = oy. 3.6. Состояния О; и Оу являются [-эквивалентными, а их *i-e преемники по отношению к любой входной последовательности длины 1 являются Й2-эквивалентными, но (21)-рэзличимыми. Покажите, что если о,- оу, то к-\-кп-\-2. 3.7. Автомат М имеет 1-эквивалентные классы Sn. 2i2, 2,г, где /=1, 2, г, содержит щ состояний. Сосчитайте число строк в таблице пар для М. 3.8. Разбиение автомата с п состояниями имеет г классов. (а) Если РкфРк-и каково минимальное число классов в Р"} (б) Если Р)1 Ф Pk-u каково максимальное число состояний в одном классе Pki (в) Каково наименьшее значение к, при котором Ptt является заведомо одинаковым с P+i? 3.9. Таблица 3 3.1 представляет собой частично заполненную Яз таблицу автомата с шестью состояниями. Определите 2-эквива-лентное разбиение этого автомата. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [ 36 ] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] 0.0019 |