Таблица 3 3.1

Таблица 3 3.2

3.10, Найдите эквивалентное разбиение автомата, определенного таблицей 3 3.2: (а) построением таблиц, (б) методом таблицы пар.

3.11. Определите эквивалентное разбиение автомата, определенного графом на рис. 3 3.2: (а) построением таблиц, (б) методом таблицы пар, (в) катричным разбиением.

3.12. Покажите, что если = и М2Ф М3, то Ф М.

3.13. -Рис. 3 3.3 представляет собой граф переходов автомата с четырьмя состояниями. Постройте граф переходов автомата с пятью состояниями, эквивалентный заданному на рис. 3 3.3.

3.14. Каждое состояниз автомата эквивалентно некоторому состоянию автомата М, но Mi Ф М. Покажите, что автомат Mi эквивалентен либо изолированному, либо тупиковому подавтомату Мг-

3.15. Пусть состояние а; автомата Mi эквивалентно состоянию Oj автомата Мг- Известно, что имеется некоторая входная последовательность, которая проводит Mi \ ai через все состояния Mi и в то же время проводит М21 о/ через все состояния М2. Покажите, что Ml = М2.

3.16. Определите, какие два из трех автоматов, показанных на рис. 3 3.4, являются эквивалентными и какие различимыми. Который из автоматов является минимальным?

3.17. Покажите, что если автомат М является тупиковым или

изолированным подавтоматом автомата М, то М содержит подавтомат М", который является минимальной формой М, либо ту-- -

пиковым подавтоматом М, либо изолированным подавтоматом М<

либо, наконец, автоматом М.

3.18. Покажите, что если М = М- ... = М, то М представляет собой минимальную форму автомата М.....iv)-

la/rPMi/ff)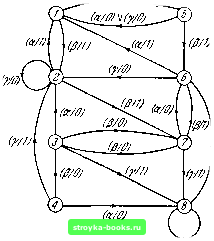

Рис. 3 3.2.

ta/mts/ff)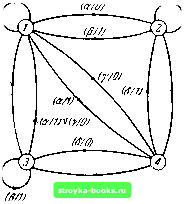

Рис. 3 3.3.

3.19. Покажите на примере, что два неминимальных эквивалентных автомата, имеющих одинаковое число состояний, не обязательно являются изоморфными.

3.20. Дано два автомата (не обязательно минимальных); сформулируйте алгоритм для определения, являютс i они изоморфными или нет.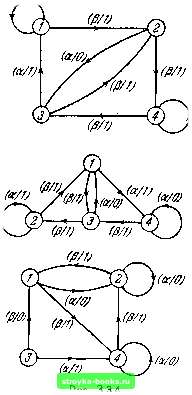

3.21. Определите минимальные формы автоматов, заданных в задачах 1.2-1.9 главы 1.

3.22. Постройте таблицу, граф и матрицу переходов минимальной формы автомата, показанного на рис. 3 3.2.

3.23. Сформулируйте правило определения всех явно эквивалентных пар состояний по таблице пар.

3.24. Получите минимальную форму автомата, изображенного на рис. 3 3.2, методом последовательного объединения, описанным в § 3.13.