Рис. 4.2. Минимальная диагностическая последовательность для \0i, aJ.

1 fe <; / - 1 lu есть входной символ, который переводит " ik-\ "Р - fe)-paзличимыx и (/-fe-1)-эк-вивалентных состояний О/ и Оу; (2) есть входной символ, при приложении которого к автоматам N[\oi и Мау- последние выдают различные выходные символы.

Определение и, о,- м Оу из а/ и ау- (1 fe •< </-1). Определение и , О/ и О/. когда О/. , и О/ известны, может быть наиболее удобно произведено с помощью таблиц Р, построение которых для эквивалентных разбиений данного автомата описано в § 3.6. сг/ и сгу являются (1 - fe + 1)-различимыми и (/ - fe)-эквивaлeнтными состояниями; следовательно, они составляют смежные строки в таблице и разобщенные строки в таблице P, +i.

Поэтому строки и Оу в таблице Pi- должны со-

держать две клетки, скажем а/ и Оу соответственно, которые имеют различные нижние индексы, по меньшей мере в одном, скажем , -м столбце. При этом о! и о

ДЛЯ автомата M\aj, где (фТЦ. Используя обозначения рис. 4.2, можно установить, что если и Оу, /-различимы и (/ - 1)-эквивалентны и если lulu есть минимальная

диагностическая последовательность для {о;,, OyJ, то: (1) для

\ \ \ \

l-pajMVi/m/ (1-1)-рами¥шы 2 - разливши Л

4.4] Эксперименты для двух состоянии 129

должны быть (/ - k-1)-эквивалентными, так как они являются первыми преемниками (/ - А)-эквивалентных состояний О/ и Oj относительно входного символа ; они

должны быть также (Z-ft)-различимыми, так как а и о

имеют различные нижние индексы в таблице /-*j j. Следовательно, а. и о. являются искомыми состояниями Oi k-l k-l *

и О; соответственно, и входной символ \ есть искомый ft

входной символ и. Таким образом, и, о,- могут

быть определены путем просмотра таблицы /-*; j.

Определение Ц из Oi и Oj . 0/ и <У] являются 1-различимыми; поэтому должен существовать, по крайней мере, один входной символ, при приложении которого к автоматам M\oi и M\Oj последние выдают различные выходные символы. Этот символ, который является искомым символом „, может быть легко определен путем нахождения в Zy-подтаблице столбца, в котором строки аг и <jj различны.

Приведенные методы могут быть объединены и представлены в виде следующего алгоритма.

Алгоритм 4.1. а/„ и Oj суть два состояния автомата М. Чтобы определить минимальную диагностическую последовательность для {а,„, OyJ: (1) Построим таблицы для М. Найдем / такое, что а,-„ и Оу, являются смежными строками в таблице и разобщенными строками в таб-

лице Р,. Предположим, что ft=:l. (2) (а) Если I - ft > О, то переходим к шагу 3. (б) Если I - ft =- О, то соответствует любому столбцу в Zy-подтаблице М, такому, что строки О/ и О/ в этом столбце различны, lu.lu, lu. есть минимальная диагностическая последовательность для Oi, Oj. (3) соответствует любому столбцу в таблице Pi~k< такому, что строки Oi и Oj этого столбца имеют клетки Oi и Oj соответственно с различными нижними индексами. Увеличиваем ft на единицу и возвращаемся к шагу (2).

Для иллюстрации рассмотрим автомат Л17, представленный таблицей 4.1 и изображенный на рис. 4.3. Таблицы 4.2 - 4.5 являются таблицами Рр Р, Р и Р4 автомата Л17. Для примера найдем минимальную диагностическую последо-

вательность для (1,2}, т. е. У (1,2). Начнем с рассмотрения таблицы Р3, так как это «последняя» таблица, в которой строки 1 и 2 являются смежными. Строки 1 и 2 в таблице Pj имеют различные нижние индексы в клетках «4» и «5», которые находятся в столбце р. Значит, р есть первый символ в (1.2). В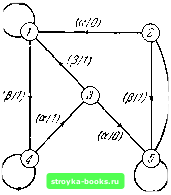

таблице строки 4 и 5

различные в

имеют различные нижние «3ft» и

«2д», которые находятся в столбце а. Значит, а есть второй символ в (1.2). В таблице Р, строки 3 и 2 .f J имеют различные нижние индексы в клетках «5» и «1а», которые находятся в столбце а. Значит, а есть третий символ в (1,2). р также может быть выбран в качестве третьего символа, так как строки 3 и 2 имеют различные нижние индексы в клетках «1,» и «5», которые находятся в столбце р. В Zy-подтаблице строки 1 и 5 имеют различные клетки (О и 1) в столбце а. Значит, а есть четвертый и последний символ в (1,2). Таким образом, (1,2) имеет

Рис. 4.3. Автомат АП.

Таблица 4.1 Автомат АП

Таблица 4.2 Таблица Pi для А\7