Таблица 4.3 Таблица Pj для А\7

Таблица 4.4 Таблица Р, для АП

Таблица 4.5 Таблица P4 для AM

Таблица 4.6

Минимальные диагностические последовательности для пар состояний А\1

вид рааа или papa. Когда рааа прикладывается к Л17 в состоянии 1 и в состоянии 2, последний выходной символ есть 1 и О соответственно, что легко может быть проверено по таблице 4.1 или по рис. 4.3. Следовательно, если {1,2) является множеством допустимых начальных состояний Л17, то диагностический эксперимент может быть проведен путем приложения рааа и наблюдения последнего выходного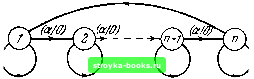

(т (рт (0/0) WO)

Рис. 4.4. Автомат А\Ь.

стигнута для любого п. Очевидно, что в Л18 никакие два состояния не могут выдать различные выходные символы прежде, чем будет достигнуто состояние п из одного из этих состояний и приложен входной символ а; следовательно, Диагностический эксперимент для Л18 и допустимого множе-

символа: если этот символ-1, то начальное состояние - 1, если этот символ-О, то начальное состояние - 2. В таблице 4.6 перечислены все минимальные диагностические последовательности для всех пар состояний {о,„, Од) Л17; последние два столбца в этой таблице указывают последние наблюдаемые выходные символы tj и Zv, когда минимальная диагностическая последовательность прикладывается к о и Оу„ соответственно. Хотя для данной пары состояний могут быть построены две или более минимальных диагностических последовательностей, в таблице приведена только одна такая последовательность.

4.5. Разновидности диагностической задачи с двумя состояниями

Следующая теорема суммирует рассуждения, приведенные в предыдущем параграфе.

Теорема 4.1. Диагностическая задача для автомата, содержащего п состояний, с двумя допустимыми состояниями всегда может быть решена простым безусловным экспериментом длины I, где

1п - \. (4.1)

Рис. 4.4, на котором изображен автомат Л18, показывает, что верхняя граница в соотношении (4.1) может быть ,п,о-

4.5) РАЗНОВИДНОСТИ ДИАГНОСТИЧЕСКОЙ ЗАДАЧИ Ш

ства {1,2) не может быть короче, чем п-1. Минимальная диагностическая последовательность для {1,2} состоит из последовательности п - 1 символов а, выходная последовательность оканчивается нулем, если начальное состояние -1, и единицей, если начальное состояние -2.

Диагностическая задача для двух состояний прямо связана со следующей задачей: известно, что данный автомат М является либо автоматом в состоянии о, либо автоматом в состоянии Oj, причем имеются таблицы переходов М, и Ml, М2 являются сравнимыми автоматами. Желательно распознать автомат и его начальное состояние. Простым искусственным приемом рассмотрения М как расщепляемого автомата М и Жд, а именно .{М, Жд), указанная задача может быть перефразирована в следующем виде: известно, что данный автомат {М, М), таблица переходов которого доступна, находится в одном из состояний о,, Оу. Найти это состояние. Эта задача в точности представляет собой диагностическую задачу для автомата Д(Ж5, Жд) и допустимого множества начальных состояний {о, Оу}. При = Оу задача может быть решена методом, описанным в § 4.4. По теореме 4.1, мы имеем:

Следствие 4.1. Известно, что данный автомат должен быть либо Ml в состоянии о,., либо Жз в состоянии Оу, где ф Oj, Ml и Жз сравнимы и их таблицы переходов доступны. Если Ml есть автомат с tii состояниями, а Жд - с состояниями, то данный автомат и его начальное состояние всегда могут быть установлены простым безусловным экспериментом длины где

<«i4-«2-l- (4.2)

Как показано на примере автоматов Л19 и Л20 (рис. 4.5), верхняя граница в соотношении (4.2) может быть достигнута в точности для любых n-i и «2. В примере предполагается, что «21 (когда я, = «2. состояние Л] в Л20 имеет единственную исходящую дугу, отмеченную (а/О) V (Р/0). которая ведет к состоянию Л; - 1). Прежде всего заметим, что никакие два состояния / в автомате Л19 и у в автомате Л20 не могут выдать различных выходных символов до тех пор, пока не будет достигнуто состояние 1 из / и у и не будет приложен входной символ р. Далее, вычеркнем в Л20 пару