
 |
|
Главная Кибернетика [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [ 42 ] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] вход-выход (а/О) исходящей из состояния дуги, обозначенной (а/О) V (Р/0). добавим к щ петлю (а/О) и рассмотрим. 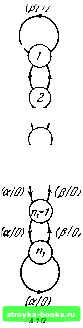 (а ?;1Л(т 3 (a/ff)(0/ff) 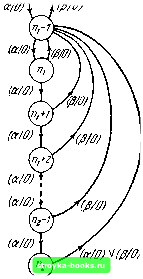 A2ff Рис. 4.5. Автоматы Л19 и Л20. как это повлияет на Л20. Как только это сделано, состояния «2 и «2 - 1 становятся явно эквивалентными и могут быть заменены одним состоянием, скажем rtj -1; состояния -1 4.6] ДЕРЕВО ПРЕЕМНИКОВ 135 И «2 - 2 ЯВЛЯЮТСЯ теперь явно эквивалентными и также могут быть заменены одним состоянием, скажем щ - 2; состояния «1+1 и «1 являются теперь явно эквивалентными и могут быть заменены одним состоянием, скажем В своей сокращенной форме автомат Л20 одинаков с Л19 и, следовательно, состояние / Л19 эквивалентно состоянию / Л20 для всех /, Поэтому можно сделать вывод, что кратчайшая входная последовательность, под действием которой Л19 и Л20 должны выдавать различные выходные последовательности, когда оба автомата находятся в начальном состоянии 1, должна переводить автомат Л20 из состояния 1 в состояние и затем входным символом а в состояние Я; - 1. Так как состояние 1 должно быть вновь достигнуто перед тем, как либо Л19, либо Л20 выдадут различные выходные символы, та же самая последовательность должна переводить Л20 из состояния в состояние 1 и затем оканчиваться входным символом р. Поэтому кратчайший эксперимент, различающий между собой Л19 в состоянии 1 и Л20 в состоянии 1, состоит в приложении символов а, за которыми следуют - 1 символов р, с общей длиной ftj 4" «2 - 1. Последний наблюдаемый символ в этом эксперименте есть О, если в состоянии 1 находится автомат Л19, и 1, если в состоянии 1 находится Л20. Следует отметить, что единственное требование, предъявляемое к Ж и в следствии 4.1, состоит в том, что О; ф Oj. Это требование не зависит от различимости или эквивалентности и М2 (О; и Оу могут быть различимыми состояниями в двух эквивалентных автоматах). Следовательно, нет необходимости распространять на расщепляемый автомат А (Ж;, М2) предположение о том, что отдельные автоматы Mi и М2 являются минимальными. 4.6. Дерево преемников В дальнейшем под а-множеством автомата М будем понимать любое конечное множество состояний М; элементы о-множества не обязательно различны ). о-множество, ) Хотя а-множество не является «множеством» в формальном смысле (так как оно содержит повторяющиеся элементы), оно будет обозначаться фигурными скобками, как это принято для обычных множеств. содержащее единственный элемент, называется простым; о-множество, содержащее два или более одинаковых элементов, называется кратным; о-множество однородно, если все его элементы одинаковы (простое о-множество является частным случаем однородного о-множества). Для автомата, у которого множество допустимых начальных состояний имеет мощность т, Л-группа есть множество о-множеств, причем т есть общее число элементов во всех входящих в Л-группу о-множествах. Число о-множеств в Л-группе называется решением группы. Решение Л-группы не может превышать т. Л-группа называется простой, если все о-множества в ней просты; Л-группа однородна, если все о-множества в ней однородны. Предположим, что О есть Л-группа, содержащая о-множества gy g.....g. ... I,- -преемник О есть другая Л-группа, построенная согласно следующим правилам: (1) Разбиваем каждое множество g на подмножества такие, что два состояния g включаются в одно и то же подмножество, если и только если они вырабатывают одинаковые реакции на входную последовательность 1.1,. •.. I, . Считаем каждое l 2 l подмножество как о-множество, а множество всех таких о-множеств-как Л-группу, обозначенную через О. (2) В о-множествах из О заменяем каждое состояние его преемником относительно входной последовательности I, I, .. . L . По- лучаемая в результате Л-группа есть • • • I; -преемник О. Дерево преемников есть структура, определенная для данного автомата М и заданного множества допустимых начальных состояний Л (Ж). Структура состоит из ветвей, расположенных в последовательных уровнях, причем высшим уровнем является «нулевой» уровень, следующим за высшим является «первый» уровень и так далее. Нулевой уровень дерева содержит единственную ветвь, называемую начальной ветвью. В дереве преемников, -noCTpoeHHOM для автомата с входным алфавитом Ц, I2.....1р]< каждая ветвь в k-м уровне (ft 0) расщепляется на р ветвей, представляющих li> 12- • • Ер соответственно и являющихся ветвями в (ft-f-l)-m уровне. Ветвь, представляющая входной символ Е;, называется «ветвь 1». Ясно, что ft-й уровень дерева содержит />* [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [ 42 ] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] 0.0013 |