эксперимент для М* и множества допустимых начальных состояний (1, 2.....т\ должен состоять из /я - 1 подпоследовательностей, совокупная длина которых задана верхней границей выражения (4.15). Автомат УИ* показывает также, что кратчайший безусловный установочный эксперимент может иметь длину (2n~tn)(m - 1)/2 символов.

Заметим, что так как конечная Л-группа на рис. 4.18 является простой Л-группой, показанный путь описывает минимальную диагностическую последовательность (так же как минимальную установочную последовательность). Поэтому автомат М* показывает, что простой безусловный или условный диагностический эксперимент может иметь длину, равную верхней границе / (4.15).

4.17. Следствия, связанные с экспериментами по распознаванию состояний

Особым случаем диагностической или установочной задачи для т состояний для автомата М является диагностическая или установочная задача для п состояний, где п есть общее число состояний в М. Эта проблема возникает, когда для М не определены допустимые состояния, и в этом случае следует предполагать, что начальным состоянием может быть любое из п состояний М. Для этого специального случая результаты, полученные в предыдущих параграфах, могут быть видоизменены и обобщены следующим образом.

Следствие 4.3. Пусть М есть автомат с я состояниями и известной таблицей переходов. Если начальное состояние автомата М вообще может быть определено путем проведения простого эксперимента, то оно может быть определено с помощью простого безусловного или простого условного эксперимента длины I, где

/<(я -1)я". (4.17)

Начальное состояние М всегда может быть определено с помощью кратного безусловного эксперимента длины I и кратности с, где

/<(я-1)2. (4.18)

f<rt-l, (4.19)

4.т7]

СЛЕДСТВИЯ, СВЯЗАННЫЕ С ЭКСПЕРИМЕНТАМИ

И с помощью сложного условного эксперимента длины / и кратности с, где

/<1«(«-1). (4.20)

с<я - 1.

(4.21)

Конечное состояние М всегда может быть определено с помощью простого безусловного эксперимента длины /, где

/<(П-1)2,

(4.22)

и с помощью простого условного эксперимента длины I и порядка d, где

/</г(я-1). d<«- 1.

(4.23) (4.24)

Пусть М - автомат с входным алфавитом {Ij, I2.....\р]

и множеством состояний (Oj, Oj. о„). Состояния Оу и {1ф У) называются совместимыми, если реакции М \ Oj и M\ai на одинаковы и если Oj и имеют одного и того же преемника по отношению к li. Пара 1-совместимых состояний изображена на рис. 4.19.

Теорема 4.14. Пусть М есть автомат с п состояниями и входным алфавитом x = \ii, I2. U-

(а) Если М содержит пару li-совместимых состояний для каждого входного символа I; из X, то диагностическая задача для п состояний для М никогда не можетбыть решена простым экспериментом, (б) Если М не содержит пары li-совместимых состояний ни для какого входного символа из X, то диагностическая задача для п состояний для М всегда может быть решена простым экспериментом.

Доказательство, (а) Подача любого входного символа на М заставляет пару состояний, скажем Оу и о, перейти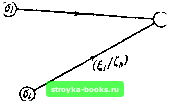

Рис. 4.19. Пара -совместимых состояний.

В ОДНО и то же состояние с одинаковыми реакциями и, таким образом, обусловливает то, что эти состояния становятся не различимыми никакими последующими входными символами, (б) По теореме 4.12, М всегда может быть переведен в известное конечное состояние. Пусть установочной последовательностью, примененной для этой цели, является 1,1, .. . I, ;

пусть соответствующая выходная последовательность будет t,hy .....Сл а соответствующая последовательность состояний Oj, Oj, .... Oj. Предположим теперь, что Oj, и 1, известны для некоторого k, 1 <; ft г; так как

по предположению ни одно состояние в Л1 не имеет двух заходящих дуг, несущих одну и ту же пару вход-выход {1 lh ) •О у может быть определено однозначно. Обозначим начальное состояние М через О;,, тогда Оу„ может быть определено рекурсивно на основе знания KOHe4Hofo состояния М и входной и выходной последовательностей, включенных в установочный эксперимент.

Из таблицы переходов заданного автомата М может быть легко установлено, обладает М свойством, упомянутым в части (а), или свойством, упомянутым в части (б) теоремы 4.14. Поэтому эта теорема оказывается во многих случаях полезной для того, чтобы установить, может ли начальное состояние заданного автомата быть определено с помощью простого эксперимента. Когда автомат не имеет ни свойства части (а), ни свойства части (б), то его начальное состояние либо может, либо не может быть определено простым экспериментом.

Задачи

4.1. Опишите матричный способ решения диагностической задачи для двух состояний.

4.2. Таблицы 3 4.1 и 3 4.2 соответственно представляют автоматы А тл В. Перечислите минимальные диагностические последовательности для всех пар состояний, в которых одно состояние выбирается из А, а второе состояние -из В.

4.3. Рис. 3 4.1 показывает граф переходов автоматов А л В. (а) Известно, что заданный автомат есть А в состоянии 3 или 4. Постройте кратчайший безусловный эксперимент для распознавания начального состояния, (б) Известно, что заданный автомат есть А р состоянии 1 или В в состоянии 1. Постройте кратчайший без-