8.2) ОБЩАЯ ЗАДАЧА РАСПОЗНАВАНИЯ АВТОМАТА 185

стояний автомата будет множество возможных, физических состояний пациента. В данном примере диагностическая задача состоит в том, чтобы определить болезнь, с которой поступил больной (т. ё. определить «начальное состояние»). Как мы установили ранее, эта задача не всегда разрешима: возможно, что природа болезни такова, что, независимо от предписанного лечения, болезнь исчезнет раньше, чем будет установлена. Установочная задача в рассматриваемом примере состоит в том, чтобы вылечить пациента, т. е. перевести его в известное физическое состояние (т. е. «конечное состояние»). Как мы ранее установили, эта задача всегда разрешима. Всегда имеется последовательность назначений, которая обязательно переведет пациента в известное физическое состояние (конечно, не обязательно желаемое). Задача распознавания автомата в данном примере состоит в определении того, как настоящая реакция и будущее физическое состояние пациента связаны с назначенным в настоящее время лечением и настоящим физическим состоянием (т. е. в определении «таблицы переходов»). Ясно, что до тех пор, пока не будут установлены указанные зависимости, не могут быть проведены какие-либо серьезные диагностические процедуры или назначено лечение. Поэтому определение физиологических характеристик пациента, которые могут быть" установлены на основании сведений о его возрасте, поле, роде занятий, перенесенных болезнях, должно предшествовать любым действиям, имеющим целью управление здоровьем пациента.

5.2. Общая задача распознавания автомата

Будем говорить, что автомат является распознанным, если определена (с точностью до изоморфизма) его минимальная форма путем измерений на его внешних выводах. Будем говорить, что автомат распознаваем, если он может быть распознан независимо от его начального состояния. Задача распознавания автомата в ее наиболее общей форме состоит попросту в следующем: распознать заданный автомат М. Ниже в этом параграфе мы покажем, что если об автомате М нет достаточной информации, то общая задача распознавания автомата неразрешима.

Теорема 5.1. Автомат М нераспознаваем, если заранее не известен полностью его входной алфавит.

Рис. 5.1. Автоматы Afj и Afj к теореме 5.1.

Рассмотрим теперь автомат М2 (также показанный на рис. 5.1), отличающийся от Alj только тем, что в Ж2 к петле или исходящей дуге всех состояний добавлена пара вход-выход (Ir/Sr), где I, принадлежит X, но не принадлежит X. Поскольку реакции и Alj на последовательность одинаковы, то в результате указанного эксперимента может быть сделан вывод о том, что автомат М - это автомат М2, с такой же уверенностью, как и вывод, что автомат М- это Ml- Однако, так как автоматы М-у и М2 не сравнимы, то они, конечно, не эквивалентны, и, следовательно, предположение о том, что эксперимент выявляет минимальную форму, не может быть доказано. Тогда от противного следует, что если входной алфавит автомата М не полностью известен, то автомат М не может быть распознан.

Теорема 5.2. Автомат М нераспознаваем, если предварительно не известно максимальное число состояний минимальной формы этого автомата.

Доказательство. Пусть некоторым экспериментом произвольной, но конечной длины L установлено, что является минимальной формой автомата М, показанной на рис. 5.2. Пусть автомат имеет множество состояний [а, 05, - а„}. Рассмотрим автомат М2 (также показанный на рис. 5.2),

Доказательство. Предположим, что исследователю известно только подмножество, скажем X, входного алфавита X автомата М. Предположим также, что некоторый эксперимент, использующий входную последовательность , символы которой выбираются из подмножества X, выявляет, что М имеет минимальную форму М., показанную на рис. 5.1.

----@ < ©---

5.2]

ОБЩАЯ ЗАДАЧА РАСПОЗНАВАНИЯ АВТОМАТА

построенный В соответствии со следующими правилами. Автомат М2 имеет n(L-\-l) состояний о, oj,). Если пара вход-выход обозначает дугу, ведущую

от состояния О; к состоянию Oj в автомате М, то в автомате Ж2 пара также

обозначает дугу, ведущую из состояния а,,„ в

состояние а.

i + (u-l)n для И = 1,

0-©-

----Ur„

----л

J + un

2..... L; если к автомату Жз в состоянии о приложен входной символ то выходной символ будет и следующее состояние будет a„. Тогда по построению каждая входная последовательность длины L или меньшей вырабатывает одинаковые выходные последовательности в Mil а,- и в MjIo,!. Однако если прикладывается любая входная последовательность длины i + 1 к >Ij I а,, и к Жз!,. то две выходные последовательности этих автоматов должны различаться последними символами. Таким образом, результат любого конечного эксперимента над автоматом Ж может быть одинаково присущим как Ж], так и Ж2, хотя и Ж2 не эквивалентны. Следовательно, автомат Ж не может быть распознан никаким конечным экспериментом. Заметим, что если известно максимальное число состояний п автомата Ж, то автомат Ж2 исключается экспериментом длины L такой, что (L--l)«>«- Таким образом, если п известно, то с помощью достаточно длинного эксперимента автомат Ж может быть распознан.

Итак, можно считать установленным, что необходимым условием распознавания автомата является предварительное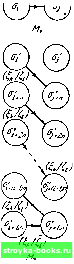

Рис. 5.2. Автоматы Af, и к теореме 5.2.