
 |
|
Главная Кибернетика [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [ 62 ] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] Теперь задача определения повреждения в автомате Л24 сведена к задаче определения конечного состояния поврежденного автомата Л24 или к задаче проведения установочного эксперимента над автоматом Д (Л24, А24", А24"). (а/и 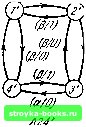 (a /)W/V (a/V (a/V (a/mm 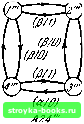 (a 7J /124" Рис. 5.3. Автомат Д (Л24, A2V, A24"). Эксперимент для распознавания повреждения описан в таблице 5.7, где предполагается, что начальным состоянием Таблица 5.6 Автомат Д (Л24, А24", А24")
автомата Л24 является состояние 2 и что в результате повреждения при приложении к автомату входного символа а в состоянии 4 на выходе получается 1. Тогда истинным автоматом является Л24", а истинным начальным состоянием- 2" (это, конечно, экспериментатору сначала не известно). Первый столбец таблицы 5.7 содержит в качестве руководства читателю истинное состояние А2\" на различ- ЗАДАЧА РАСПОЗНАВАНИЯ ПОВРЕЖДЕНИИ Таблица 5.7 Эксперимент по распознаванию повреждения в автомате А24
Установочный эксперимент для А2А и {Г, 2, 3, 4} 2" 1" 2" {V, 2, 3, 4} {Г, 3} {2} 1, 2 1, 3 Установочный эксперимент для А24" и (1", 2"} 3" {1", 2"} {1"} (1", 2"} Установочный эксперимент для A2V" и {!", 2", 3", 4"}
ных стадиях эксперимента по распознаванию. В соответствии с алгоритмом 5.1 сначала проведем регулярный условный установочный эксперимент для автомата Л24 с множеством допустимых начальных состояний {!, 2, 3, 4). В конце этого эксперимента оказывается, что если испытуемый автомат есть автомат Л24, то его конечным состоянием должно быть состояние 2. Далее проводим регулярный условный установочный эксперимент для Л24" с множеством допустимых начальных состояний {1", 2"). В конце этого эксперимента может быть сделано заключение о том, что если испытуемый автомат есть А24", то его конечным состоянием должно быть 1". Затем проводим регулярный условный установочный эксперимент для автомата Л24" с множеством допустимых начальных состояний [I", 2", 3", 4"), который устанавливает, что конечное состояние должно быть 1", если испытуемым автоматом является А24". Тогда в конце третьего установочного эксперимента заданным автоматом может быть Л24 в состоянии Г (ааа переводит 2 в 1) или Л24" в состоянии Г" (аа переводит 1" в 1"), или Л24" в состоянии Г". Поэтому далее проводим регулярный условный установочный эксперимент для автомата А (Л24, Л24", Л24") с множеством допустимых состояний {!, 1", 1"), который выявляет, что конечным состоянием является 4". Так как состояние 4" принадлежит подавтомату /424", эксперимент показывает, что испытуемым автоматом является Л24". Таким образом, можно сделать заключение, что имеющее место повреждение вызывает появление 1 вместо О при приложении входного символа а к автомату Л24 в состоянии 4. Заметим, что уменьшение длины распознающего эксперимента достигается в том случае, если после приложения каждой подпоследовательности возможно больше состояний автомата Д (Л24, Л24", Л24") исключается из рассмотрения в качестве конечных. Например, после приложения первым входного символа р и получения 1 на выходе состояния 2", 2" и 4" (в дополнение к состояниям 2 и 4) могут быть исключены из числа конечных состояний. В результате второй установочный эксперимент может быть опущен, а третий установочный эксперимент укорочен. 5.5. Сильносвязные автоматы В этом параграфе рассмотрим важный класс автоматов, называемых «сильносвйзными автоматами». Определение 5.1. Автомат М с множеством состояний {oi, 02.....о„} называется сильносвязным, если существует входная последовательность, которая переводит автомат М из любого заданного состояния а, в любое заданное состояние Oj (где / может равняться у). Из определения следует, что сильносвязные автоматы не могут содержать в себе никаких преходящих, тупиковых или изолированных подавтоматов. И наоборот, любой автомат, который содержит преходящий, тупиковый или изо- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [ 62 ] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] 0.0014 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||