последовательностью ёх или Таким образом, необходимость условия теоремы очевидна. Предположим теперь, что М не содержит состояний с потерей и что с01 наблюдается при приложении неизвестной входной последовательности к автомату М в известном начальном состоянии а. По таблице переходов определим все различные входные

последовательности, скажем j, 2.....г- которым точно

соответствует с; одной из этих последовательностей должна быть . Обозначим состояния, в которые ведет через

2l<..... r/<. (Т;, ..... соответственно.

Поскольку, согласно допущению, не является состоянием

с потерей, а, а,-.....а,- должны быть различными и,

следовательно, должно существовать взаимно однозначное соответствие между состояниями а и входными последовательностями Теперь приложим установочную последовательность, скажем j, построенную для М с множеством допустимых начальных состояний ja, а.....а;. Обозначим конечное состояние, в которое перейдет автомат после приложения через а,-, а выходную последовательность, которая получится при этом, через t. Пара последовательностей вход-выход fflMff может относиться только к одному из состояний О;, а,-.....а по следующим соображениям: допустим, что ffltH относится к двум состояниям, скажем а,- и а; тогда О; ведет в Оу через W-hI<h и через Однако, так как к - различные последовательности, это означало бы, что является состоянием с потерей, что противоречит предположению, по которому автомат М не содержит состояний с потерей. Следовательно, fflSlff однозначно определяет состояние, в которое автомат переходит из О; при приложении , и, значит, однозначно определяет . Это положение иллюстрируется рис. 5.5, где предполагается, что является действительной входной последовательностью .

Пусть 5у(а„) обозначает множество состояний, в которое переходит автомат М из состояния а„ с выходным символом у. Если М является автоматом без потери информации, имеющим р входных и q выходных символов, то множества

5i(a„), 52(а„).....qit должны содержать полное число

элементов р. Теперь пусть «множество D;j(aj)» обозначает

некоторое множество состояний, скажем Ja,, а,.....a,J,

достижимых из состояния а, с выдачей одной и той же выходной последовательности длины k. Тогда множество 5y(o,JU5y(a,JU ... U5y(o,) является множеством Djj((T,). Если М-автомат без потери информации, то число элементов множества D+j (о,)

*+1 о

элементов в множествах о

должно

равняться

числу всех

jih) •/К)-K.v) лля любого у. Таким образом, составляя рекурсивно все множества Ь,{а{) для всех Ли/, можно определить, является автомат М автоматом без потери информации или нет.

Указанный критерий может быть легко применен при построении так называемой таблицы проверки потерь. В этой таблице каждому столбцу соответствует свой, отличный от других, выходной символ Таблица делится на следующие друг за другом подтаблицы, первая из которых содержит

в основном столбце состояния Oj, .....сг„ автомата М,

а содержимым клетки, находящейся на пересечении строки а„ и столбца Су, имеет множество Sj{o,j). Клетки основного столбца (А -(- 1)-й подтаблицы заполняются содержимым клеток &-й подтаблицы, притом таким, которое не встречалось в основных столбцах предшествующих подтаблиц. В клетке на пересечении строки (piy О;.....О;) и столбца Су в (&+1)-й подтаблице записывается множество 5y(a,JU yjoJU • •• U5y(a,), которое может быть составлено по данным первой подтаблицы. Построение таблицы заканчивается при выполнении одного из следующих условий: (1) число элементов некоторого множества 5у(а„) (в первой подтаблице) меньше мощности входного алфавита; (2) число элементов некоторого множества 5y(o,j)U5y(o,jU • U5y(o,J (в ft-й подтаблице, где ft > 1) меньше общего числа элементов множеств 5у(а,, 5y(o,J, ... ..., Sy (о,); (3) нельзя добавить ни одной новой строки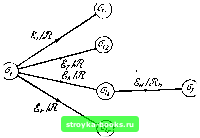

Рис. 5.5. Пояснение доказательства теоремы 5.П.

в основном столбце. Если условия (1) и (2) не имеют места, то М является автоматом без потери информации. Очевидно, что общее число строк в таблице проверки потерь не может превышать

(5.15)

Поэтому проверка потерь информации является конечным процессом.

В качестве примера в таблице 5.9 приведена таблица проверки потерь для автомата А25, заданного графом переходов рис. 5.6 и таблицей 5.8. Первая подтаблица строится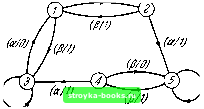

(ct/OJ

Рис. 5.6. Автомат А2Ъ.

на основании таблицы 5.8. В основной столбец второй подтаблицы переписываются из первой таблицы множества {1, 3}, {1, 5} и {2, не содержащиеся в основном столбце последней. В клетке второй подтаблицы на пересечении строки {1,5} и столбца 1, например, проставляется набор состояний, стоящих в клетках первой подтаблицы на пересечении строк 1 и 5 и столбца 1, а именно {2, 3, 4}. Остальные клетки таблицы заполняются аналогично. Так как из рассмотрения таблицы 5.9 следует, что условия (1) и (2) не имеют места, автомат А2Ъ является автоматом без потери информации.

Проиллюстрируем, как могут быть определены входные последовательности автомата без потери информации. Пусть известно, что автомат А2.Ъ до приложения неизвестной входной последовательности находился в состоянии 1, а в результате приложения этой последовательности выдал выходную