Таблица 5.! Автомат А2Ъ

Таблица 5.9

Таблица проверки потерь для автомата А2Ъ

последовательность 111. Из графа переходов, изображенного на рис. 5.6, можно заключить, что последовательность 111 может соответствовать входным последовательностям ара, арр и аар, которые переводят автомат из состояния 1 в состояния 2, 3 и 4 соответственно. Последовательность ар является установочной последовательностью для автомата А2Ь с множеством допустимых состояний {2, 3, 4}. При приложении последовательности ар в состояниях 2, 3 и 4 выходные последовательности будут соответственно 11, 01 и 10. Следовательно, истинной входной последовательностью будет ара, арр или аар, в зависимости от того, какая будет реакция автомата на последовательность ар (приложенную после неизвестной входной последовательности)- 11, 01 или 10 соответственно.

Автомат М без потери информации можно рассматривать как канал связи, в котором сообщение, переданное на входном конце, принято в закодированной форме на выходном конце. Задача декодирования получаемого сообщения может быть успешно разрешена, если получатель знает состояние канала перед передачей каждого сообщения и если канал может быть переведен в известное конечное состояние после

передачи каждого сообщения. Если получатель не может контролировать передающий конец (как это часто имеет место), то второе требование может быть удовлетворено, если отправитель «согласится» закапчивать каждое сообщение последовательностью т. е. заранее определенной установочной последовательностью для автомата М и для множества допустимых начальных состояний содержащего все состояния автомата. Например, для автомата А25 и для множества допустимых состояний {1, 2, 3, 4, 5} установочной последовательностью будет ааа. Если отправитель систематически заканчивает каждое сообщение передачей последовательности ааа (или передает ааа в течение определенных, заранее оговоренных интервалов времени), то все переданные сообщения могут быть расшифрованы на приемном конце без необходимости доступа к входным зажимам автомата. Л1ожно также показать, что если отправитель согласен передавать последовательность перед каждым сообщением, то принимающему не нужно знать начальное состояние М (т. е. состояние М, в котором к М был приложен первый символ ссоэ-щения), так как это начальное состояние можетбыть определено по реакции автомата на Таким образом, если до и после каждого сообщения передается последовательность то это сообщение -может быть расшифровано с помощью только таблицы переходов М. В нашем случае это означает, (

что передача каждого сообщения должна начинаться \/\ и заканчиваться передачей

входной последовательности у \(рт(Г/Ф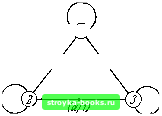

Рис. 3 5,1.

Задачи

5.1. Постройте автомат, от которого никаким эксперимен- (y/JJ том длины 4 нельзя отличить автомат, изображенный на рис. 3 5.1, но который не эквивалентен этому автомату.

5.2. Известно, что минимальный автомат М имеет два состояния, входной алфавит {а, р} и выходной алфавит {О, 1}. Известно также, что ни одно из состояний автомата М на графе переходов не имеет петель. Опишите эксперимент, распознающий этот автомат, если его истинное представление такое, как показано

В таблице 3 5.1, и если его действительное начальное состояние 1 (которое сначала ие известно).

5.3. Известно, что автомат, определенный таблицей 35.2, неисправен и что в результате неисправности, по крайней мере, вместо одной из «1» вырабатывается «О». Опишите эксперимент, распознающий повреждение, состоящее в том, что в состоянии 1 вместо «1» иа выходе вырабатывается «О», и если.начальным состоянием автомата является состояние 3 (что сначала ие известно).

Таблица 3 5.1

Таблица 3 5.2

Рис. 3 5.2.

5.4. На рис. 3 5.2 показан неполный граф переходов автомата с двумя состояниями. Опишите эксперимент над автоматом, с помощью которого можно закончить построение графа переходов. Предположите, что искомая дуга обозначается (а/1) и ведет в состояние 1 и что начальным состоянием автомата является состояние 1 (которое сначала ие известно).

5.5. Покажите, что автомат М с множеством состояний S =

когда G (а,) в § 2.6.]

5.6. Покажите, что для того, чтобы автомат Af с п состояниями был сильиосвязиым, необходимо и достаточно, чтобы матрица

2 [Щ не имела нулевых элементов. *=1

5.7. Автоматы Af, и Afj являются сильиосвязными и состояние а,- автомата Af, эквивалентно состоянию Oj автомата Мг. Покажите, что Af, = Afj.

5.8. Постройте автомат с п состояниями, который является сильиосвязным, но ие содержит ни одного полного контура.

5.9. Автомат Af имеет множество состояний S= [ои а,..., а„}. Покажите, что: (а) Af является обратимым, если в каждом изолированном подавтомате автомата М имеется состояние такое, что

„] является сильиосвязным тогда и только тогда, S для 1=1, 2,..., п. [Определение G (а,) дано