Тогда алфавит s, обозначаемый через 5, определяется формулой

S=Y. (1.16)

Выражения (1.13) и (1.14) можно теперь записать так:

z = f,{x, s). (1.18)

Из (1.15) и (1.17) получаем:

= (1-19)

Как теперь видно, уравнения (1.18) и (1.19) выражают искомые характеристические функции. Следовательно, 5 составляет требуемое для описания заданной системы множество состояний.

Для примера рассмотрим схему, показанную на рис. 1.4. На вход Увх от источника поступают импульсы со значением О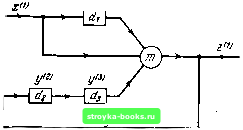

Рис. 1.4. Схема с мажоритарным элементом.

и 1 со скоростью один импульс в каждые Т секунд. Тактовые моменты выбраны совпадающими с моментами появления импульсов. Элементы rfj, d, d - задержки, которые запоминают поступающие на них импульсы на Т секунд и затем передают их на следующий за ними элемент. Элемент т представляет собой «мажоритарный орган», который выдает импульс О или 1 в зависимости от значения (О или 1 соответственно) большинства поступающих на его входы импульсов. Нас интересует значение импульса на выходе v. Значение импульса на входе схемы v,. в момент можно

1.9] другая модель 27

принять в качестве входной переменной д;*, а значение импульса на выходе Увых в момент - в качестве выходной переменной г*. Значения импульсов, запомненные элементами rf], й?2 и з- в момент можно принятЬ в качестве зависимых переменных з») соответственно. Тогда имеем:

-={0. 1}. Z={0. 1}.

5= {(ООО). (001). (010), (011). (100), (101), (110), (111)).

Из схемы видно, что у = д;0), yW=2) и у= у {, значение г) равно значению большинства переменных уЧ,, аг*

и Ууь Используя эти соотношения, можно определить значения функций:

у1" = :(Ч". yf-v У%)

y? = g,{x. У%. УЬ- yiii).

y<f = 3K-ii-l:-ytii>

Результаты вычислений представлены в таблице 1.1. Из определения 5 следует, что каждая строка части таблицы, состоящей из столбцов yly и yf , представляет собой состояние 5.,, а каждая строка части таблицы, состоящей из столбцов .уЧ и уз) - состояние sy Учитывая, что = и = z, можно сделать вывод, что таблица 1.1 полностью описывает характеристические функции рассматриваемой схемы. Например, из таблицы легко определить (см. четвертую строку), что при состоянии в настоящий момент (001) и входном символе в этот же момент 1 выход в настоящий момент будет 1, а следующее состояние (ПО).

1.9. Другая модель

Любой конечный автомат, соответствующий основной модели, задаваемой определением 1.1, может быть преобразован в автомат, в котором выходной символ в настоящий момент является функцией только состояния в настоящий момент. Преобразование может быть выполнено путем определения

Функции gk для системы рис. 1.4

переменной s как упорядоченной пары (л;.,, s). Алфавит 5 переменной s, следовательно, определяется выражением

S=X®S. (1.20)

Используя уравнение (1.5), представим в виде

Из определения s и уравнения (1.6) получаем выражение для s;j:

<+: = /;К+г <) (l•з)

Уравнения (1.21) и (1.23) определяют вторую модель конечного автомата, в которой состояние однозначно опреде-

Таблица 1.1