6.4]

ОПРЕДЕЛЕНИЕ ПАМЯТИ АВТОМАТА

являются элементами множества Qi\ По матрице [Mf и диаграмме переходов для автомата М может быть построена таблица, в которой у-й столбец содержит элементы QJ; если нет двух столбцов, имеющих общий член, то k должно быть памятью автомата М.

В качестве примера рассмотрим автомат Л28, показанный на рис. 6.6. Матрица переходов автомата Л28 задана

Таблица 6.3

Множества <?*/ для Л28

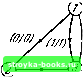Рис. 6.6. Автомат АШ.

выражением (6.23), а матрица переходов первого порядка - выражением (6.24).

[Л28] = 2 3 4

" О О

(1/0) О О О

О/О (1/1)

О (0/1) V (1/1) О О

4 О О

(0/1) (0/1) V (1/1)

. (6.23)

[Л28] =;

(6.24)

По (6.24) и (6.23) можно построить таблицу 6.3, в которой

перечислены Q1*. Qf\ Qf* и Q<,*.

Так как последовательности вход-выход (0/1) и (1/1) появляются в двух различных столбцах этой таблицы, память автомата Л28 будет превышать 1. Выражение (6.25)

представляет собой матрицу переходов второго порядка для автомата Л28.

По (6.25) и (6.23) можно построить таблицу 6.4, в которой перечислены Q". Qf\ Qf и Q[K

Таблица 6.4 Множества 0*2* для Л28

Автомат Л28 должен иметь память 2, так как никакая последовательность вход-выход не появляется в двух различных столбцах этой таблицы. Если бы автомат Л28 не был автоматом с конечной памятью, то этот факт обнаружился бы из таблицы, перечисляющей Qe\ Qi\ Qi и

6.5. Минимальная д;-0-функция

Если известна память ji конечного автомата М, то автомат может быть охарактеризован уравнением вида

2v = /(-v -v-i.....-v-u- v-v .....•2v-f;)- (6-26)

Функцию /, соответствующую выражению (6.26), будем называть х-г-функцией автомата М. Часто аг-2-функция содержит целый ряд несущественных переменных и может быть сведена к виду

Zv = f{Xv-i, X-i.....X-i, Zv-yj, Z-].....v-yj.

(6.27)

6.5]

МИНИМАЛЬНАЯ д;-г-ФУНКЦИЯ

где 0<;i < /2 < .. . < iuJ<Ji < Л < • • • <Jv lu = \ и (или) Д = М- Функция / называется минимальной x-z-функцией М, если u--v-минимальное число аргументов х и Zi, необходимых для выражения z, как функции входных воздействий и выходных реакций в форме (6.27). Таким образом, минимальная дг-г-функция получается из дг-г-функ-ции путем вычеркивания из последней максимально возможного числа аргументов х и Zf. Получение минимальной аг-2-функции, или минимизация аг-2-функции представляет интерес для целого ряда задач анализа и синтеза, когда для заданного конечного автомата желательна наиболее компактная форма его описания, т. е. форма (6.27).

Задача минимизации аг-2-функции может быть сформулирована более точно на языке аг-2-таблицы, общая форма которой показана в таблице 6.5.

Таблица 6.5

Общая форма дс-2-таблицы

Таблица разделена на q групп строк, по одной группе для каждого выходного символа в выходном алфавите {Ci, С2. • • • С] автомата Men состояниями. Группу строк, обозначенную в столбце z символом будем называть t,,i-zpyn-

пой. Столбцы х , z , ..... v-l.

заполняются следующим образом. Пусть (j/Cft) является парой вход-выход, связанной с дугой, которая начинается в состоянии О;, и пусть • ••