1) Материал этой главы частично базируется на работах Ауфенкампа (Р. D. А U f е п к а m р, Analysis of Sequential Machines, IRE Trans., vol. EC -7, pp. 299-306, 1958), Гинзбурга (S. Gins burg, A Technique for the Reduction of a Given Machine to a Minimal - State Machine, IRE Trans., vol. EC - 8, pp. 346-355. 1959; S. 0 i n s-b u r g, On the Reduction of Superfluous States in a Sequential Machine, J. Assoc. Comput. Mach., vol. 6, pp. 259-282, 1959) и Паула и Ангера (М. С. Р а и 11 and S. Н. U п g е г, Minimizing the Number of States in Incompletely Specified Sequential Switching Functions, IRE Trans., vol. EC -8, pp. 356-367, 1959).

В следующих параграфах мы увидим, как некоторые понятия и методы, развитые в предыдущих параграфах, могут быть распространены на класс автоматов с ограничениями на входе

7.2. Совместимость состояний

При определении основной модели с конечным числом состояний (см. § 1.6) молчаливо предполагалось, что характеристические функции Д и Д конечного автомата определены для каждой пары {х, s). При изучении автоматов с ограничениями на входе удобно видоизменить эту модель и допустить наличие пар {х, s), для которых обе функции Д и Д остаются неопределенными. В частности, мы можем предполагать, что Д и Д у автомата не определены для пары (Ij, Ol), где Ij - входной символ, а о, - состояние автомата М, если ни при каких условиях Ij не может быть приложен к Жа,; при этом говорят, что автомат М имеет ограничение на входе в состоянии о. В таблице переходов автомата М такое ограничение отмечается тем, что клетки в обеих подтаблицах и .yj, расположенные на пересечении строки / и столбца у, остаются пустыми (или заполняются прочерками). Входная последовательность называется допустимой в состоянии о, если при приложении к Жа, она не нарушает ограничения на входе ни в каком состоянии автомата М. В качестве примера на рис. 7.1 и в таблице 7.1 представлен автомат Л32 с ограничениями на входе.

Состояния Ol и Оу автомата М с ограничениями на входе называются совместимыми, если для Жа, и M\aj при подаче на вход любой допустимой для о, и Оу входной последовательности на выходе появляется одна и та же

7.21

СОВМЕСТИМОСТЬ СОСТОЯНИИ

последовательность. Состояния и Oj несовместимы, если существует, по крайней мере, одна входная последовательность, допустимая как для О;, так и для Oj, при подаче которой на M\ai и M\aj автомат выдает различные выходные последовательности. Видно, что совместимость обладает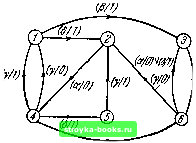

fa/mm

Рис. 7.1. Автомат АЪ1.

свойствами рефлексивности и симметричности, но не обладает свойством транзитивности, так как последовательности, допустимые для О; и Оу, не обязательно допустимы для Оу и Oj.

Таблица 7.1

Автомат i432

-v+1

Совместимость поэтому нельзя понимать как обычное отношение эквивалентности, а следует относить только к парам состояний.

Следует заметить, что определение совместимых пар состояний совпадает с определением эквивалентных пар состояний, если на входные последовательности рассматриваемого автомата не накладываются никакие ограничения. Таким образом, определение совместимости пар состояний может быть получено из определения эквивалентности пар состояний, если в последнем (см. определение 3.1) выражение «любой входной последовательности» заменить выражением «любой входной последовательности, допустимой для обоих состояний» (это изменение не отразится на правильности определения 3.1, так как в автомате без ограничений на входе множество допустимых последовательностей составляет множество всех последовательностей). Поэтому определение пары совместимых состояний производится так же, как определение пары эквивалентных состояний, с той лишь разницей, что все последовательности, недопустимые для обоих состояний пары, не учитываются,

В § 3.7 был описан метод, названный методом таблицы пар, для определения всех эквивалентных пар состояний в данном автомате. В соответствии с приведенными замечаниями этот метод может быть использован для определения всех совместимых пар состояний при условии, что первый вариант таблицы пар видоизменяется следующим /эбразом; (1) элементы в столбце пар представляют собой пары состояний, при которых выдается один и тот же выходной символ при подаче любого входного символа, допустимого для обоих состояний пары; (2) если входной символ недопустим для обоих состояний Ol и Oj, то клетка, расположенная на пере-сеченш} строки (о, Oj] и столбца д, в таблице пар остается

Таблица 7.2

Таблица пар для автомата А32