между применением этого метода для автоматов без ограничений на входе и применением его для автоматов с ограничениями на входе состоит в том, что в последнем случае содержимое незаполненных клеток таблицы, содержащих прочерк, можно интерпретировать произвольно.

В качестве примера в таблицах 7.5 и 7.6 представлены соответственно таблица Pi и таблица Рг автомата Л32, заданного таблицей 7.1. Таблица получена путем замены прочерков в клетках подтаблицы таким образом, чтобы

Таблица 7.5 Таблица Pi для А32

Таблица 7.6 Таблица для А32

множества (1, 2, 3, 5) и (4, 6} стали 1-эквивалентным разбиением. Заметим, что возможны также другие замены прочерков в клетках, но при выбранной замене получается наименьшее число классов 1-эквивалентности. Таблица Pg получена заменой прочерков в клетках таблицы Pj таким образом, что множества (1, 2}, (3, 5} и (4, 6} становятся 2-эквивалентным разбиением. Так как это - конечная таблица Ру, то является эквивалентным разбиением, из которого сокращенная форма может быть построена по алгоритму 7.2. Случайно получилось, что множества {1, 2}, (3, 5) и (4, 6} также составляют минимальную правильную группировку, так что сокращенный автомат, полученный на основе Pg, является также минимальной формой автомата Л32 (действительно, это автомат Л321 рис. 7.2). Заметим, однако, что другая замена прочерков клеток в таблице Pj может

7.61 МЕТОД УМЕНЬШЕНИЯ ЧИСЛА СОСТОЯНИЙ 261

1), {2, 3, 5 2. 3. 5). {4

в результате дать 2-эквивалентное разбиение 4, 6), затем 3-эквивалентное разбиение {1}, . 6 и, наконец, эквивалентное разбиение {1}, {2}, (З, 5 4 , {6}. Ясно, что последнее разбиение дает менее удовлетворительную минимизацию автомата Л32, чем (1, 2}, (3, 5}, (4, 6}. В общем случае целесообразно пробовать несколько различных замен на каждом шаге процесса разбиения и изучать, как влияют различные замены на число классов, получаемых при окончательном разбиении или, по крайней мере, при разбиении, непосредственно следующем за данным. Замена прочерков должна быть выбрана так, чтобы дать наименьшее число классов.

Преимущество описанного метода состоит в том, что он позволяет использовать личную изобретательность и опыт для получения сокращенных форм за относительно малое время. Недостатком его является то, что он не гарантирует уменьшения числа состояний и, конечно, не гарантирует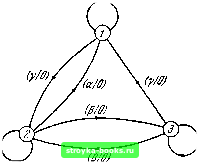

(r/oj "

Рис. 7.4. Автомат у133.

минимизации заданного автомата. Важно отметить, что минимальная форма не гарантируется этим методом даже в том случае, если перепробованы все возможные замены прочерков в клетках на каждом шаге описанной процедуры. Причина состоит в том, что каждое эквивалентное разбиение неизбежно составляется из непересекающихся классов эквивалентности, в то время как минимальная правильная

группировка может быть образована из пересекающихся совместимых множеств. Например, рассмотрим автомат ЛЗЗ, представленный графом на рис. 7.4 и таблицей 7.7. Р, в этом случае будет {1, 2}, {3}, или {1,3}, {2}. В каждом из этих случаев Pg будет {1}, {2}, {3), а это означает, что ЛЗЗ не может

быть минимизирован предложенным методом. С другой стороны, если применить общий метод минимизации, то окажется, что {1, 2} и {1, 3} являются С-множествами для ЛЗЗ

Таблица 7.7 Автомат ЛЗЗ

ф/ОМу/Ю

(с[/т(у/{)

Рис. 7.5. Автомат ЛЗЗ.

и что эти два С-множества составляют правильную группировку. Поэтому ЛЗЗ имеет минимальную форму ЛЗЗ, которая состоит из двух состояний. На рис. 7.5 приведена эта минимальная форма, в которой состояния 1 и 2 представляют соответственно множества {1, 2} и {1, 3} автомата ЛЗЗ.

Задачи

7.1. Покажите, что не существует множества в минимальной правильной группировке, которое можно было бы включить в какое-либо другое множество этой группировки..

Таблица 3 7.1