7.2. Cl, Cj.....Ch представляют собой все С-множества автомата М с ограничениями на входе. Покажите, что Cj. С2.....Сд

составляют правильную группировку и, следовательно, что число

состояний в Л1 не может превышать А.

7.3. Первый вариант таблицы пар для автомата с шестью состояниями представлен таблицей 3 7.1. Найдите все С-множества и минимальную правильную группировку для этого автомата.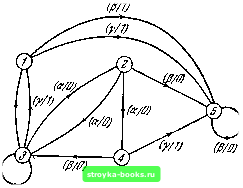

Рис. 3 7.1.

7.4. Найдите минимальную форму автомата, заданного таблицей 3 7.2.

Таблица 3 7.2

7.5. Определите минимальную форму автомата с ограничениями на входе, изображенного на рис. 3 7.1.

7.6. Уменьшите число состояний автомата, заданного таблицей 3 7.3. используя метод сокращения, описанный в § 7.5.

Автоматы с ограничениями на входе [гл. 7

Таблица 3 7.3

БИБЛИОГРАФИЯ!)

Айзерман М А., Гусев Л. А., Розоноэр Л, И., Смирнова И. М., Таль А. А., Конечные автоматы, Автоматика И телемеханика, т, XXI, №№ 2, 3, 1960.

Aufenkamp D. D., Analysis of Sequential Machines, IRE Trans., vol. EC-7, pp. 299-306, 1958. [Русский перевод; Ауфен-к a м п Д. Д., Анализ последовательностных машин, II, Сб. переводов «Математика», 3 : 6, 1959.]

Aufenkamp D. D. and Н о h n F. Е., Analysis of Sequential Machines, IRE Trans., vol. EC-6, pp. 276-285, 1957. [Русский перевод: A у ф e н к a м п Д. Д., X о н Ф. Е., Анализ последовательностных машин, 1, Сб. переводов «Математика», 3; 3, 1959.]

Bellman R., Sequential Machines, Ambiguity and Dynamic Programming, J. Assoc. Comput. Mach., vol. 7, pp. 24-28, I960.

Bellman R., Adaptive Control Processes, pp. 119-123, Princeton University Press, Princeton, N. J., 1961. [Русский перевод: Белл-м a н P., Процессы регулирования с адаптацией, «Наука», 1964.]

Bennett W. S., Minimizing and Mapping Sequential Circuits, Trans., AIEE, vol. 74. pt. 1, pp. 443-447. 1955.

Блох A. Ш.. Эквивалентные преобразования последовательностных машин, Автоматика и телемеханика, т. XXI, № 11. 1960.

Burks А. W.. The Logic of Fixed and Growing Automata. Annals of the Computation Laboratory, vol. 29, pp. 147-188, Harvard University Press, Cambridge, Mass., 1959.

Burks A. W. and Wang H.. The Logic of Automata. J. Assoc. Comput Mach.. vol. 4. pp. 193-218, 279-297, 1957.

Burks A. W. and Wright J. В., Theory of Logical Nets, Proc. IRE, vol. 41, pp. 1357-1365, 1953. [Русский перевод: Б ер к с А., Райт Дж., Теория логических сетей, «Кибернетический сборник», № 4, ИЛ, 1962.]

С а d d е п W. J., Equivalent Sequential Circuits, IRE Trans., voL CT-6, pp. 30-34, 1959.

de Bruijn N. G., A. Combinatorial Problem, Proc. Ned. Acad. Wetensch., vol. 49, pp. 758-764, 1946.

E 1 s p a s В., The Theory of Autonomous Linear Sequential Networks. IRE Trans., vol. CT-6, pp. 45-60. 1959.

Fitch F. В., Representation of Sequential Circuits in Combinatory Logic, Phil., Sci., vol. 25, pp. 263-279, 1958.

Friedland В., Linear Modular Sequential Circuits. IRE Trans., vol. CT 6, pp. 61-68, 1959.

) Библиография ограничена статьями и книгами, в которых непосредственно рассматриваются вопросы, затрагиваемые в этой книге.