
 |
|
Главная Методы условной оптимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [ 10 ] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] 2.2.6. МНОГОМЕРНАЯ ГЕОМЕТРИЯ В ЭТОМ разделе рассматриваются геометрические характеристики векторов X, удовлетворяющих равенству ах=р, (2.48) где а= (с,, Oj, . . ., а„) - некоторый ненулевой вектор, ар - число. Введем множество векторов г, для которых а?=(1. Они формируют линейное векторное пространство размерности п-1 (нуль-пространство вектора а). Через 2={г,, Zj, . . ., z„.i) обозначим его ортонормальный базис. Поскольку вектор а лниейно независим от {«1, Za.....z„ i}, присоединение его к Z дает базис для SR". Соответственно каждь1й вектор х представим в виде x=aiZs+a.gZg+. . .-)-а„ ,г„ ,-)-а„с, (2.49) а для X, удовлетворяющих (2.48), получим ах=ааа=, откуда „ = Ё п пТа ~ IIQ II? • Множество всевозможных векторов вида (2.49), где значение а„ фиксировано, называют гиперплоскостью, вектор а-ее нормалью, а вектор аоЩ единичной евклидовой длины-единичной нормалью. Гиперплоскость можно представлять себе как результат переноса (п- 1)-мерного подпространства, ортогонального вектору а, в направлении, параллельном этому вектору. Заметим, что при р=0 гиперплоскость проходит через начало координат, т. е. совпадает с этим подпространством. В противном случае расстояние от произвольной точки X гиперплоскости до начала координат ограничено син.зу положительной величниой. По определению квадрат этого расстояния равен xtx = a\ + ai-{- ... +a.l (аТа). т. е. минимальное значеине последнего равно ipi/llQlla и достигается при «1=. . .=п„ 1=0 (когда X пропорционален а). Для наглядной иллюстрации рассмотрим множество двумерных векторов, определенное равенством GX=CiXi--CaX2=P, где Qi=l, Qj=-I, Р=-1/2. Оно изображено на рис. 2d штриховой линией. Заметьте, что вектор о=(1, -1) ортогонален гиперпло-
Рис. 2d. Гиперплоскость в двумерном случае. скости (в данном случае оиа представляет собой прямую), н кратчайшее расстояние от иее до начала координат равно 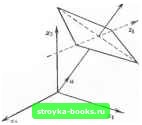 На рис. 2е изображена гиперплоскость в трехмерном случае. Обратите внимание, что векторы г,, г, . . ., z„ i могут интерпретироваться как оси ортого- нальной системы коорди-нат, лежащей в гиперплоскости и имеющей началом ее точку, ближайшую к исходному началу координат. Различные значения Р при фиксированном сбудут давать параллельные гиперплоскости. Преобразование переноса можно применить к любому по.пространству S, определив множество всех векторов вида x„+i/, где/g, а х„-фикснро- Рис 2е. Гиперплоскость в трехмерном ванный вектор. Такие мно- случае, жества называют линейными многообразиями. Гиперплоскость есть особый случай линейного многообразия, характерный тем, что размерность S равна п - 1. Замечания и избранная библиография к разделу 2 Есть много вводных курсив по вычислительной линейной алгебре; см., например, Стюарт (1973), Стренг (1976) и соответствующие главы в книге Дальквиста и Бьёрка (1974). Более специальные и сложные вопросы рассматриваются в книгах Форсайта и Молера (1967) и Лоусона и Хансоиа (1974). Подробности методов обновления матричных разложений пока еще не просочились в учебники. Однако заинтересованный читатель может найти их в статьях Гилла, Голуба, Мюррея и Сондерса (1974), Дэниела, Грэга, Кауфмана и Стюарта (1976). Зрелому математику мы рекомендуем в качестве источника, содержащего полный и тщательный обзор основополагающих сведений по вычислительной алгебре, книгу Уилкинсона (1965). К настоящему времени разработано большое количество высококачественных программ для решения задач линейной алгебры. Первоклассными источниками их могут послужить книги Уилкинсона и Райнха (1971), Смита и др. (1974), Доигарра, Банча, Молера и Стюарта (1979). 2.3. ЭЛЕМЕНТЫ МНОГОМЕРНОГО АНАЛИЗА 2.3.1. ФУНКЦИИ многих ПЕРЕМЕННЫХ; ЛИНИИ УРОВНЯ В последующих разделах рассматриваются основные свойства скалярных функций многих переменных, используемые при построении оптимизационных алгоритмов. Эти функции будем обозначать через F(x), где х - вещественный п-мерный вектор (х,, х., . . ., ХтУ, во всех случаях, кро- Рис. 2f. Контурный график функции f И=е>.(4л:;+2х+4х,хИ-2хг+1). ме одного, когда /г=1. Б этом случае для обозначения функции будет использован символ f(x), а индекс едииствениой компоненты аргумента х, как правило, будет опускаться. Ниже встретятся также векторные функции - упорядоченные наборы скалярных функций векторного аргумента х, компоненты которых независимо от размерности X будут обозначаться через (х). В дальнейшем везде, где это целесообразно, обсуждение функций многих переменных сопровождается иллюстративными примерами для случаев малой размерности. В частности, используются так называемые контурные графики. Для произвольной функции f (дг) векторного аргумента А6 уравнение г=--Р(х) определяет в («+1)-мерном пространстве 54"+ некоторую гиперповерхность. Когда п = 2, это-обычная поверхность в трехмерном пространстве (г, х,. х. При этом для каждого с из множества значений функции F (х,, х уравнение F(x,, хс неявно задает кривую в координатах х,, Xg на плоскости г = с. Если несколько таких кривых, соответствующих некоторой выборке значений параметра с, изобразить иа одной плоскости, получится контурный график функции. Образующие его кривые принято называть линиями уровня. На рнс. 21 представлен контурный график функции F (х) = с*. (Ах\ -f 24 -- 4xiX2 -)--I-2x-j-)-l). Показаны линии уровня, отвечающие значениям с, равным 0.2, 0.4, 0.7, 1., 1.7, 1.8, 2.8, 4, 5, 6 и 20. 2.3.2. НЕПРЕРЫВНЫЕ ФУНКЦИИ И ИХ ПРОИЗВОДНЫЕ В основе подавляющего большинства методов решения оптимизационных задач лежит идея использования информации о функции в точке для прогноза ее поведения в целом. Мы рассмотрим сей-  Рис. 2g. Разрывная функция. час некоторые свойства функций, позволяющие делать подобные прогнозы. Центральным среди них является непрерывность. Функцию одной переменной называют непрерывной в точке х, если для любого наперед заданного числа е(е>()) можно найтн число 6 (6>0), такое, что при всех у, удовлетворяющих неравенству 1/-х<6, будет справедливо неравенство 1/(41-/(х)<е. Геометрически непрерывность f в точке X означает, что график f Нх) выглядит «над хг как слитная кривая. Функцию /, не удовлетворяющую данному определению, называют разрывной в х. Значение такой функции в х может сильно отличаться от ее значений в соседних с х точках (см., например, рис. 2 g). Чтобы дать строгое определение непрерывности в многомерном случае, введем понятие окрестность точки «-мерного пространства. Пусть 6 - некоторое положительное число. Тогда Ь-окрестностыо точки х назовем множество всех точек у, удовлетворяющих иеравеиству \\у-хЦб. Какую именно норму использовать в этом определении, как правило, не существенно, хотя от этого, разумеется, зависит «форма» окрестности. Чаще всего берут евклидову норму. Б трехмерном случае определение 6-окрестности с евклидовой нормой задает шар радиуса 6 с центром в х. Когда ясно, о какой величине б идет речь либо эта величина не играет роли, вместо хб-окрестность» говорят просто «окрестность». Приведенное выше определение непрерывности функции одной переменной непосредственно обобщается на многомерный случай переходом от интервалов значений скалярного аргумента к б-окрестностям значений векторного аргумента. Соответственно скалярная функция F{x) векторного аргумента х называется непрерывной в точке X, если для любого t:>0 найдется 6>0, такое, что при всех у, удовлетворяющих иеравеиству \\у-х<6 (т. е. лежащих в б-окрестиости х), будет If (х)-f (j/)l<e. Если же непрерывной называют векторную функцию, то имеют в виду, что непрерывны все ее скалярные компоненты. Отметим, что заключение о непрерывности или разрывности функции F в точке х не зависит от того, какая норма будег использована для измерения разности у-х. Это может повлиять только на выбор конкретных значений 6. На контурном графике функции двух переменных ее разрыв проявляется «слиянием» разных линий уровня (например, в точке «вертикального обрыва» поверхности z=F(xi,x). Следующее важное свойство функций-дифференцируемость. Начнем с определения его в одномерном случае. Для этого рассмотрим график функции f на интервале, содержащем некоторую точку X. Выберем на этом же интервале еще одну точку у {уфх) н построим отрезок, соединяющий в плоскости графика точки с координатами (х, f(x)) и (у, f(y)). Тангенс угла наклона этого отрезка к горизонтали равен „г(у) = 1М=Л±, У-" Если он имеет предел при стремлении у к X, этот предел, равный тангенсу угла между горизонталью и касательной к графику в точке х, называют первой производной илн градиенпюм от / в х. Для обозначения первой производной используют символы /(х), (х) или df/dxlY. Формально Рис. 2h. функция / (X) = lim т (у) = lim n+M-fix) (2.50) Когда /х) существует, функцию / называют дифференцируемой в точке X. Рис. 2h иллюстрирует сказанное на примере функции f(x) = x, точки х = 1 и интервала [-2, 2]. При любом h для /(х) flx+h)-f(x) x+2hx+h-x- , Л--h-= х + п. (2.51) Предел (2.51) при Л О существует при всех х и равен / (х) = 2х. Следовательно, f (1) = 2. Существование производной, определенной соотношением (2.50), означает, что величина т (у) стремится к одному и тому же пределу независимо от того, с какой стороны у приближается к х! Однако может случиться так, что предел для т{у) будет существовать только при стремлении у к х с одной стороны либо значения пределов при приближении к х слева и справа будут различными. Возьмем, например, непрерывную функцию / (х) = х, изображенную иа рис. 2i. Очевидно, что ее наклон равен - 1 для х<0 и равен +1 для х> 0. В точке х = 0 будет т{у) = ~1, если у<х, и т(у) = -1, еслн у> х. Соответственно предела (2.50) для функции /(х) = х при х = 0 иет, т. е. в начале координат она иедифференцируема. Чтобы полисе описывать рассмотренные случаи недифференцируемости, вводят понятие односпюронние производные. Когда существует предел lim (2.52, его называют производной справа от функции / в точке х и обозначают через f (х). Аналогично определяется производная слева. Это-предел, отличающийся от (2.52) заменой условия f(y /1 > О на /1 < 0. В предыдущем примере с/(х) = х обе односторонние производные существуют во всех точках и совпадают везде, за исключением начала координат. Коль скоро функци я / диф-ференцируе.ма в любой точке некоторого интервала, ее производную / можно рассматривать иа нем как новую функцию скалярного аргумента х. Последнюю естественно обозначить через / (х); в этом контексте запись „(х)" означает ие какую-то фиксированную точку, как прежде, а независимую переменную. Если функция / (х) в свою очередь окажется дифференцируемой в точке X, ее первую производную называют второй производной от / в X и обозначают через /" (х), f" (х) или dfldx\j. Возвращаясь к примеру с f(x) = x, легко убедиться, что вторая производная /" определена для всех х и постояииа:  Рис. 21. Функция f(x)=\x\. f- {х+Щ-Г(х) 2x+2h-2x h h Понятно, что начатый процесс дифференцирования производных можно продолжать и дальше, пока определены соответствующие пределы. Тем самым вводится понятие п-й производной функции / в точке X, которую принято обозначать через (х) или d"fldx" \у. Читателю, не знакомому с основами дифференцирования, следует заглянуть в какой-нибудь учебник по математическому анализу, где он найдет правила дифференцирования суммы, произведения и частного. Здесь мы ограничимся чем, что приведем без доказательства общее правило дифференцирования сложной функции g(f(x)). Оно заключается в том, что при определенных необременительных ограничениях на /, g и х справедлню равенство r,g(f(x)) = gif{x))f(x). [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [ 10 ] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] 0.0757 |