
 |
|
Главная Методы условной оптимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [ 12 ] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] ошибка имеет второй порядок малости и определяется значениями в некоторых точках отрезка [x-h, х+Л]. Заметим, что для расчета нового приближении производной требуются значения функции в двух дополнительных точках, а не в одной, как для правой и левой аппроксимаций. Таким образом, повышение точности аппроксимации достигнуто ценой привлечения дополнительной информации, и это - общее правило. Чтобы проиллюстрировать применение конечно-разностных формул, paccMoipHM функцию f{x)=x с производной f {х)=3х. Правая аппроксимация дает в данном случае оценку f (х), равную так что ошибкой отбрасывания будет 3xh+h. Если же воспользоваться центральной аппроксимацией, то в качестве оценки величины Зх получим ЙГ~ ~ % и здесь ошибка есть просто Л=. Тейлоровское разложение функции / позволяет строить формулы аппроксимации конечными разностями ее произюдиых не только первого, но и более высоких порядков. Например, сложение (2.61) и (2.62) дает равенство nx-f.)-y д где слагаемое 0(h) включает f". Его левая часть может служить приближением второй производной с ошибкой порядка ft, а оценка величины f"{x) с ошибкой О (ft) вытекает из равенства ~ if {x + 2h)-f (x + h)-f {x-li) + f (x-2ft)) = Г (x) + 0(h). Для того чтобы строить формулы конечно-разностной аппроксимации высших производных, нужны определения разностей высших порядков. Конструкцию таких формул и определений проиллюстрируем на простейшей схеме аппроксимации ft-й производной. Для этого введем оператор Д вычисления правой разноапи: Af{x)=f{x+h)-Hx). Здесь ради краткости записи зависимость Д от ft не указывается. Результат двукратного последовательного применения этого оператора назовем разностью второго порядка. Если и для нее ввести свой оператор, то его естественно обозначить через Д: Д V {х)=Д {Af (х))=Д/ (x+h)&f {x)=f (x+2h)-2f {x+h)+f (x). Аналогично вводятся и разности более высоких порядков. Чтобы получить наглядную интерпретацию этих формул, обозначим через fl величины f(x+jh) и сведем значения A/j в таблицу разностей вида Тогда правило их вычисления можно сформулировать так: для подсчета очередной разности в таблице надо взять две смежные разности из предыдущего столбца и вычесть верхнюю нз нижней. Можно показать, что справедливо равенство Д*/„ = ftf *(х) --0(ft*+). Соответствеиио, построив таблицу разностей по значениям f(x + jh), / = 0, 1, .... /г, мы можем оценить f *(л;) так: /""(x)~(l/ft)A Формулы конечно-разностной аппроксимации производных известны и для функций многих переменных. Пусть Л,- илтервал конечной разности, связанный с /-Й компонентой аргумента х, и cj- вектор, /-Я компонента которого равна единице, а все остальные - нулю. Тогда F(x + V/) = F{x) + h/g W Е/ + Ще]С (x + l:),hfy) e,, где 0<:fi,< 1. Слагаемые g(-r)e,- и e]G (x + QJi/ej)Ci суть не что иное, как ;-я компонента вектора g (л:) и /-Й диагональный элемент матрицы G(x + U,h,e,) соответственно. Поэтому gi(x)=ij(F(x + h/e,) -F(x)) + 0 (ft,), и ето - аналог равенства (2.58), порождающий формулы правой аппроксимации компонент градиента. Левая и центральная конечно-разностные аппроксимации величины gj(x) равны (f (x)-f (x-hf,)). (f (x + h,.e,)-F (x-ft,.,-)). Как и в одномерном случае, можно построить коиечио-разност-ные приближения вторых производных. В частности, приближением первого порядка для С,;(х) будет щ(Р(х + h/e, + Л л) - f (X + ft/,) - f (X + ft,-e,) + F (x)). Эта формула есть результат аппроксимации /-го столбца матрицы С(х) вектором (1/ft,) (g(x--ftj«j)-g(.v)) с последующей заменой компонент векторов g(x+hje,) и g(x) соответствующими разностями первого порядка. 2.3.6. СКОРОСТИ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ Подавляющее большинство методов оптимизации относится к классу итеративных. Это означает, что с их помощью генерируются бесконечные последовв!ельиости приближений {х} иско.чого решения х*. Прн этом работоспособность метода еще не гарантирована доказательством сходимости соотвегсгвующей последовательности - нужна определенная скорость сходимости. В данном разделе будут кратко рассмотрены формальные средства, которыми можно характеризовать эти скорости. Последующее изложение не претендует иа полноту, но самые важные понятия теории сходимости в нем освещены (более глубокие знания можно почерпнуть нз КИНГ, указанных в библиографии). Хотелось бы сразу оговориться, что следствия общей теории сходимости на практике должны использоваться с большой осторожностью. Так, например, нельзя оценивать алгоритмы только по величинам теоретических скоростей сходимости генерируемых ими последовательностей - хотя эти скорости в определенной степени отражают эффективность методов, условия, прн которых оии достижимы, реализуются редко. Точно так же нельзя пренебрегать алгоритмом лишь по той причине, что теоремы о скорости его сходимости не доказаны: это может объясняться низким качеством метода, но не исключено, что доказательства нет просто потому, что провести его очень сложно. Дальнейшие рассмотрения относятся к последовательности {л;}, сходящейся к х*. Чтобы упростить изложение, мы предположим, что вес ее элементы различны и ни одна из точек х ие совпадает с X*. Наиболее эффективный способ оценивания скорости сходимости состоит в сопоставлении качества приближения Xt+г с качеством приближения Xf, т. е. в измерении отношения расстояния между x+i и X* к расстоянию между х и х*. Последовательность {хц) называется сходиценся с порядком г, если г - максимальное число, для которого Поскольку величина г определяется предельными свойствами {Xf}, ее иногда называют асимптотической скоростью сходимости. При г= I говорят о линейной сходимости а прн г=2 - о квадратичной. Для последовательности {х} с порядком сходимости г вводится понятие «асимптотический параметр ошибки» - это число вида (2.64) Когда л=1, параметр у должен быть строго меньше единицы; иначе сходимости не будет. Чтобы проиллюстрировать данные определения, рассмотрим две характерные последовательности. Первая задается формулой х, = с, (2.65) где с-константа, удовлетворяющая условию 0<с<1. Каждый следующий член этой последовательности равен квадрату предыдущего, а ее предел равен нулю. При этом так что скорость сходимости г в данном случае равна двум. Квадратичная сходимость, грубо говоря, означает, что с каждым шагом число правильных цифр у Xj удваивается. Первые четырнадцать членов последовательЕЮсти (2.66) с параметром с=0.99 вынесены во второй столбец табл 2а. Обратите втгимание, что удвоение числа правильных Ш5фр начинается не сразу, а, точнее, прн А7. Вторая модельная последовательность определяется формулой У, = с-\ (2.66) где cJsO. Каждый член этой последовательности является квадратным корнем предыдущего. Ее предел при любом ОО равен 1. причем Mm - = lini -зёп;-= -J- Таким образом, эта последовательность сходится линейно. Ее начальные члены при с=2.2 выписаны в третьей колонке табл. 2а. Таблица 2а. Примеры квадратичной, линейной и сверхдннейной сходимостей
Гл. 2. Оснти Заметим, что примерно через каждые три итерации в приближении й появляется дополнительная правильная цифра. Для линейно сходящейся посипедовательиости пошаговое уменьшение нормы \\х-х*\\ существенно зависит от величины асимптотического параметра ошибки. Если этот параметр оказывается иу-левЕ.1М, говорят, что последовательность сходится сверхлинейно. Вообще сходящейся сверхлинейно называют любую последовательность, для которой предел (2.64) равен нулю. Ясно, что пол это определение попадают все последовательности со скоростями сходимости больше единицы. Проиллюстрировать сверхлинейн5ю скорость сходимости при /•=! можно на примере такой последовательности: Предел 2j равен нулю, и 1ш]£*±1 = 1т, /г(1--1/*)«+> = (2.67) Первые девять членов этой последовательности представлены в четвертой колонке табл. 2а. Замечания и избранная библиография к разделу 2.3 Полное изложение материала, которому был посвящен данный раздел, можно найти в любом учебнике по математическому анализу, см.. например, Курант (1936) и Апостол (1957). Формализм скоростей сходимости подробно рассмотрен в книге Ортеги и Райи-болдта (1973). ГЛАВА 3 Из.юженш вопроса будет неполным, пот е той или иной форме мы не оговорим всех условий Джои Стюарт Милль (1846) 3.1. ОПРЕДЕЛЕНИЕ МИНИМУМА Как было сказано в гл. 1, задачей оптимизации называется задача поиска минимума скалярной функции на множестве значений ее аргумента, удовлетворяющих некоторым ограничениям. В основном речь пойдет об ограничениях, которые выражаются в терминах соотношений иа значение непрерывных функций от переменных задачи; другие типы ограничений будут рассмотрены в гл. 7. Нам предстоит обсудить весьма широкий класс задач, именуемых нелинейными задачами ус.говной оптимизации. Ставятся они след5тощим образом: NCP найти minf (х) лей" при ограничениях c,.(x) = 0, t=l, 2.....m"; с,(х)590, i = m+\, т. Произвольную точку X, удовлетворякжцто всем ограничениям NCP, будем называть допустимой. Множества всех допустимых точек называют допустимой областью. Например, в двумерном случае единственное ограничение х, -Н Xj = О задает допустимую область, которая представляет собой прямую, изображенную на рис. За штриховой линией; если это ограничение заменить неравенством Xj+X:!, допустимой областью станет также изображенный на рис. За круг единичного радиуса (заодно проиллюстрирован и принятый в данной книге способ пометки внешней стороны р„с. За. Ограничения x,4-Xj=0 и *?+х<1. границы множества, заданно- xf--4<l 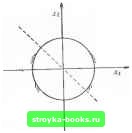 го неравенством: с этой стороны наносится штриховка). В дальнейшем используется термин „недопустимая задача". Это-задача, у которой нет допустимых точек. УСЛОВИЯ ОПТИМАЛЬНОСТИ [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [ 12 ] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] 0.001 |