
 |
|
Главная Методы условной оптимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [ 15 ] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] Займемся теперь иеобходпмьми условиями оптимальности второго порядка. Так как в точке минимума х* должно выполняться равенство Zg(x*) = f3, тейлоровское разложение (3.11) принимает вид F (x* 4-Е2рг) = F (л;*) + eplZC (х + еОр) Zp. (3. И) Соответствеино, рассуждая тем же путем, что и в случае с безусловным минимумом, нетрудно показать, что наличие у матрицы Z"G (л:*) Z отрицательных собственных значений приводило бы к существованию в лкбой окрестности х* допустимых точек с меньшими значениями F. Следовательно, в оптимальной точке X» задачи LEP матрица ZG (л;*) Z должна бьп-ь положительно полуопределенной. Это и есть искомое условие. Фигурирующую в нем матрицу принято называть спроектированной матрицей Гессе. Важно от.метить, что положительной полуопределенности самой матрицы Гессе G {х*) здесь не требуется. Чтобы проиллюстрировать применение условий второго порядка, рассмотрим двумерную задачу минимизации функции - xl + xi при ограничении x,= \. В этом случае elx) = <-2x, 2х,). Л = (0, 1) и «М-(-0 2)- Легко проверить, что равенство (3.13) выполнено с Х = Ч в точке х= (О, 1), которая тем самым претендует на оптимальность. Однако для любого вектора р = (6. Of, где 6-произвольное ненулевое число, имеем Лр = 0 и pG (j?) р = -26" < 0. Таким образом, в точке х локального минимума нет. Итак, получены следующие необходимые условия существования в точке X* локального минимума задачи LEP. Необходимые условия оптимальности для задачи LEP Е1. Ах*Ь. Е2. ZV{j<:*) = 0, или, что то же самое, g(x*) = AK*. ЕЗ. ZH} (x*)Z положительно полуопределена. Достаточные условия оптимальности для задачи LEP выводятся почти тем же способом и выглядят почти так же, как полученные ранее условия для задачи без ограничений. Только теперь в них будрт фигурировать не обычные, а спроектированные фаднент и матрица Гессе. Достаточные условия минимума для задачи LEP FI. Дх*==Ь. F2. Zg(A:) = 0, или, что то же самое, g (х) = Ах*. F3. PG (х*) Z положительно определена. 3.3.2. ЗАД.1ЧИ С ОГР.АНИЧЕНИЯ.МИ ТИПА ЛИНЕЙНЫХ HlP.XBEHCTB 3.3.2.1. Общие условия оптимальности. Рассмотрим задачу, все ограничения которой заданы линейными неравенствами: найти minf (х) при ограничениях Лх>Ь. Как и в случае с ограничениями-равенствами, вывод условий оптимальности начнем с поиска удобного способа описания всех допустимых точек, лежащих в окрестности исследуемой. Прн этом будем проводить четкое различие между теми из ограничений, которые выполняются как равенства, и теми, которые выполнены как строгие неравенства. Ограничение о,?"х>:Ь/ называют активным (или сдерживающим) в допустимой точке X. если ajxbj, и неактивным, если afx>bi. В том н другом случае говорят, что ограничение соблюдено. Если же atx<bj, ограничение называют нарушенным в х. Активные ограничения представляют особый интерес потому, что только они определяют множество возможных перемещений около допустимой точки. Если ;-е ограничение неактивно в точке x, ненулевой шаг ил х, не нарушающий этого ограничения, можно сделать в любом направлении, т. е. при любом р и достаточно малом е точка i-l-ер будет удовлетворять неактивному ограничению. Таким образом, неактивное ограничение может препятствовать только «большим» перемещениям. Иначе дело обстоит с акпшным ограничением: оно сокращает возможности перемещений в любой окрестности допустимой точки. Допустим, что i-e ограничение оказалось активным в х, т. е. ajx = bi. Тогда по отношению к нему есть две категории возможных направлений. Во-первых, возможными являются все направления р, удовлетворяющие равенству аТр = 0. Их называют удерживающими относительно i-ro ограничения, так как последнее сохраняет активность в .любой точке вида х--ар, где а-произвольное число. Говорят, что точка, движущаяся вдоль удерживающего направления, остается «на» ограничении. Во-вторых, возможны движения вдоль р, таких, что afp > 0. Эти направления называют не удерживающими по отношению к i-му ограничению. Поскольку af {х + ар) = Ь,- + аа[р > Ь,- при к > О, i-e ограничение становится неактивным в точке х + ар. Соответственно говорят, что шаг вдоль неудерживающего направления уводит «с» ограничения. На рис. 3h изображены некоторые из возможных отиоснтельно ограничения х,-)-х,> 1 направлений в допустимой точке х = Чтобы выяснить, является ли точка х* оптимальной в задаче LIP, необходимо прежде всего идентифицировать активные в ней ограничения. Определяющие их t строк матрицы Л сгруппируем в новую матрицу Л, н пусть Ь-вектор, полученный выборкой соответствующих компонент Ь. Тогда Лх* = Ь, причем строки Л расположим с учетом нх первоначального упорядочения в матрице Л так, что элементами аГ будут коэффициенты «первого» активного ограничения. Для упрощения выкладок предпо-•2 ложим, что этн строки линейно независимы; тем не менее условия, которые мы получим, сохраняют силу и в отсутствие у А полного строкового ранга. Через Z обозначим матрицу, чьи столбцы формируют базис в подпространстве векторов, ортогональных строкам Л. Тогда векторы р, удовлетво- ряющие равенству Лр = 0, можно I, будет представлять в виде линейных комбинаций столбцов Z. Рассмотрим тейлоровское раз- з:t+X2= Р„с. 3h. Возможные направления для ложение функции F около точки линейного ограничения xi+xg>\. X* ВДОЛЬ удерживающего направления p(p = Zp2): F {х- + Е2рг) = f М -Н epP-g (х«) + \ врО (х« -- евр) Zp. (3.15) Здесь 0 удовлетворяет неравенствам О < О < 1, а с-любое число. Как и в случае с ограничениями-равенствами, это разложение позволяет установить, что еслн произведение pJZg (х*) окажется ненулевым при каком-нибудь р, то в точке х* локального минимума не будет. Значит, необходимым условием оптимальности X* является равенство Z"g(x*) = 0 или, что эквивалентно. g (X*) = ЛХ. (3.16) Иногда множители Лагранжа приписывают всем ограничениям задачи, полагая их по определению равным нулю для неактивных ограничений. Мы же условн.мся вводить множители Лагранжа только для активных ограничений. Условие (3.16) обеспечивает стационарность функции F в точке X* вдоль всех удерживающих направлений. Однако возможны также движения вдоль неудерживающпх направлений, и X* заведомо ие сможет быть оптимальной точкой, если среди них найдется хотя бы одно направление убывания функции F. Ведь, еслн такое направление существует, любой достаточно малый положительный шаг вдоль него, не выводя из допустимого I М1южества, обеспечит строгое убывание значения F. Значит, если мы хотим более полно описать оптимальную точку х*, надо найти условие, которое гарантировало бы, что для всех р, удовлетворяющих неравенству Лр > О, получим g (х*)р > О, Поскольку уже известно, что вектор g(x*) есть линейная комбинация строк А с множителями Лагранжа, можно переформулировать задачу: требуется найти условие, при котором g (X)" р = Х;а1р ->-...+ Xfafp > 0,- (3.17) найдется неудерживающее на- ДгЕЯ него если только оГр>0, i= 1.....t. Оказывается, что неравенство (3.17) выполняется прн всех интересующих нас р только в том случае, когда XJO, i= 1, ...,t. Таким образом, точка х* не может быть оптимальной, если среди множителей Лагранжа есть отрицательные. Чтобы убедиться в этом, допустим, что X*-точка локального минимума (так что (3.16) выполнено), но XJ <0 прн некотором /, Тогда в силу линейной независимости строк А правление р, такое, что й[р=1; а[р = 0, (3.18) g(xVp = X-afpX}<0, и, следовательно, р является возможным направлением спуска, существование которого противоречит оптимальности х*. Значит, нз оптимальности х* в задаче LIP следует неотрицательность всех мш)жите.1ей Лагранжа. Применение этого правила знаков проиллюстрировано на рис. 31. Рассматривая тейлоровские разложения функции F в окрестности X* вдоль удерживающих направлений, можно получить условие оптимальности второго порядка, состоящее в том, что спроектированная матрица Гессе Z"G(x*)Z должна быть положительно полуопределенной. Это условие в точности аналогично условию оптимальности второго порядка для задач с ограничениями-равенствами. Суммируя сказанное выше, выпишем полный набор необходимых условий оптимальности для задачи L1P: Необходимые условия минимума для задачи LIP G1. Лх*>Ь, причем Лх*Ь. 02. Zg(x*) = 0, или, что эквивалентно, g(x*) = Л. G3. >.;>о, 1,.... t. G4. ZG(x*)Z положительно полуопределена. Перейдем теперь к выводу достаточных условий оптимальности для LIP. В сравнении со случаем, когда все ограничения имеют вид 4 Л, 2984 равенства, здесь появляется одно усложнение, и связано оно с возможностью обращения в нуль множителей Лагранжа активных ограничений. Вообще множитель Лагранжа, соответствующий ;-му активному ограничению, представляет собой оценку первого порядка для скорости изменения целевой функции прн движении вдоль тираВлеиие бЩКШпаяия F{xj 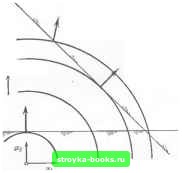 onwuKiajlbHait точка tj = agA{A> 0) Рис. 31. Применение условий оптимальности первого порадка. направления, неудерживающего относительно j-ro ограничения и удерживающего относительно всех остальных активных ограничений. Поэтому, например, положительность множителя Лагранжа означает, что при движении вдоль соответствующего направления целевая функция будет возрастать. И поэтому же равенство множителя нулю ничего ие говорит об истинном знаке изменения функции при ука.чанном перемещении, гарантируя лишь ее постоянство в линейном приближении- Отсюда ясно, что любой набор достаточных условий оптимальности для задачи LIP должен включать какие-то дополнительные требования, которые касаются направлений, не-удерживающих по отношению к активным ограничениям с нулевыми множителями Лагранжа. В подтверждение сказанного рассмотрим пример, когда из-за наличия нулевого множителя Лагранжа положительная определенность спроектированной матрицы Гессе оказывается недоста-точньЕм основанием для вывода об оптимальности точки. Возьмем двумерную задачу минимизации разности xi-xi при ограничении х,>0. В точке x = (0, 0)- имеем е(х*) = ф. Of, Л = (0, 1), Z=(l, 0)Г и ZG{x*)Z = 2. Соответственно g(х*) = Al*. где Я*=0. При этом несмотря на то, что спроектированная матрица Гессе положительно определена, локального минимума в х* нет, поскольку любой положительный шаг из х* вдоль направления (О, б), где б - положительное число, не нарушит ограничения задачи и приведет к уменьшению значения функции F. В данном случае начало координат не является точкой минимума потому, что, хотя F стационарна вдоль неудерживающего направления (О, б), ее кривизна вдоль этого направления отрицательна. Самый простой набор достаточных условий оптимальности для задачи LIP получается, если потребовать, чтобы все множители Лагранжа были положительны. Тогда возрастание F вдоль каждого из иеудерживающих направлений гарантировано, и полная сводка условий, обеспечивающих наличие в х* сильного локального минимума, будет выглядеть так: Достаточные условия минимума для задачи LIP HI. Axb, причем Ах* =1. 42. Zg{x*) = 0, или, что этивалентно, gix*) = AK*. НЗ. Я- >0, £=1.....t. Н4. ZG (х*) Z положительно определена. Потребовать положительности множителей Лагранжа - не единственный прием вывода достаточных условий оптнуальности для задачи L1P. От этого требования можно и отказаться, но тогда надо как-то усилить условие на матрицу О (л:*), чтобы обеспечить положительность кривизны F вдоль тех из возможных направлений, которые являются удерживающими только относительно ограничений с ненулевыми множителями. Например, можно выставить требование положительности кривизны F вдоль любых (независимо от допустимости) направлений такого сорта. Соответствующие условия пртшедены ниже. Если через Л. обозначить матрицу активных ограничений с положительными множителями Лагранжа, а через Z+ матрицу, столбцами которой являются векторы базиса подпространства ортогонального строкам Л + , то эти условия будут выглядеть следующим образом! Достаточные условия минимума для задачи LIP (с нулевыми множителями Лагранжа) П. Лл:*>Ь, приче.и Ах* 12. Zg (х*) = 0. или, что вквивалентно, g(x*) = АК*. 13. ?.;>о, /=1, .... t. и. ZIG ix*)Z.,. положительно определена. Заметим, что в рассмотренном выше примере данные условия не выполняются. Это естествеиио, поскольку исследуемая на оптимальность точка в действительности не оптимальна, но она станет таковой, если заменить целевую функцию иа х\-\-х\. В этом случае вновь полученные достаточные условия окажутся выполненными. Для задач с линейными ограничениями, среди которых есть н [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [ 15 ] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] 0.0011 |