
 |
|
Главная Методы условной оптимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [ 19 ] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] щую функцию, которая примет нулевое значение в некоторой точке и. Еели бы ие надо было специально заботиться о сходимости, мы просто вычислили бы!(и) и отбросили одну из старых точек, получив тем самым набор для построения следующего приближения. Однако теперь, прежде чем включать и в этот набор н вычислять f(ij), мы должны убедиться, что и - «разумная» точка. Определение «разумности» и содержит несколько требований. Во-первых, точка и должна принадлежать отрезку la, Ь]. Во-вторых, расстояние от и до лучшей из имеющихся точек должно быть меньше половины длины интервала неопределенности. Иначе шаг деления пополам скорее всего пршедет к большему сокращению этого интерва.па (т. е. второе условие нужно для гарантии того, что в неблагоприятной ситуации метод не потребует значительного увеличения количества вычислений функции по сравнению с делением пополам). Наконец, необходимо убедиться, что точка и «существенно отлична» от лучшей из предыдущих, так как если окажется, что они «численно неразличимы», то, сохранив и, нмеино по ним придется строить линейную аппроксимацию на следующем шаге, а такая аппроксимация из-за ошибок округления почти наверняка будет бессмысленной. Таким образом, мы просто потеряем этот шаг. Когда нарушается какое-нибудь из двух первых условий, и заменяют серединой интервала иеопределенносги. Если же нарушится третье, вместо и обычно берут точку, лежащую по ту же сторону от лучшей из прежних, что и и, но отстоящую от нее на фиксированное «малое» расстояние 6. При этом величина 6 не должна превосходить половины допуска на длину окончательного интервала неопределенности. Указанное правило замены приводит к тому, что два последних uiara алгоритма, как правило, оказываются «6-шагами» и точка х* локализуется иа отрезке длины 26. 4.1.2. методы одномерной минимизации Методы безусловной минимизации функции одной переменной во многом аналогичны рассмотренным выше процедурам поиска нуля. Более того, точку минимума функции f в принципе можно искать как точку ну.чя производной f с помощью любой из этих процедур. Например, деление пополам действительно привлекается иногда для этой цели. Однако, как правило, здесь разумнее обращаться к методам, специально предназначенным для задач минимизации. Первые два из представленных ниже методов поиска минимума требуют вьгаислеиий только самой минимизируемой функции и не используют значении ее производных. Они работают по принципу последовательного сокращения интерва.па неопределенности и опираются на некоторое условие, позволяющее указывать отрезок локализации минимума функции, если она унимодогьна. Есть несколько эквивалентных определений унимодальности. Одно нз иих звучит так; функция f{x) унимодальна на отрезке [а, Ь], если существует единственная точка х* g [а, Ь], такая, что для любых х,, Xag la, b] и Xi<X, f (Ч) > f (x, еьаи x, < jC; f(Xi)<f(x,). еспн Xi>x. Когда известно, что / достигает безустовного миниму.ма и унимодальна на отрезке la, Ь], положение точки минимума можно уточнить. а ц XI ь а Рис. 4е. Сокращение интервала неопредсчениосги для унимодальной функции. вычислив f в двух внутренних точках отрезка. Например, в ситуации, изображенной на рнс. 4е, по значениям / в х, их, можно утверждать, что м»шимум реализуется на отрезке 1х,, Ы. 4.1.2.1. Поиск Фибоначчи. Для построения конкретного метода одномерной минимизации, работающего по приншшу последовательного сокращения интервала неопределенностн, надо задать правило выбора на каждом шаге двух внутренних точек. Конечно, желательно, чтобы одна из них всегда использовалась в качестве внутренней и для следуюи[его интервала. Тогда частота вычислений функции сократится вдвое и одна итерация потребует расчета только одного нового значения f. Стратегией, обеспечивающей максимальное гарантированное сокращение интервала иеопределенносги при заданном количестве вычислений функции и соответственно претендующей на «оптимальность», является поисх Фибоначчи. Эта стратегия опирается на чиспа Фибоначчи {Fi), которые вырабатываются реку1)рентной формулой вида Fn = Fi=l. Начальными членами последовательности {F,] будут I, 1, 2, 3. 5, 8, 13.....При фиксированном количестве N обращений к процедуре расчета функции поиск Фибоначчи состоит в просмотре точек, дробящих интервалы неопределенности в отношениях, задахгаых числами Ff, 2.....Точнее говоря, если принять длину ис- ходного интервала за fл, то длиной /г-го интервала будет f,v ft. а его оцениваемые внутренние точки будут отстоять от левой границы на f и (, в и на f ,v t-i. причем в одной из них значение/ всегда известно из предыдущего шага. Проще всего эта процедура выглядит в случае, когда предполагаются только два вычисления функции. но не требующую задания длины окончательного интервала неопределенности процедуру. Ее называют методом золотого сечения. Можно показать, что Рис. 41, Точки поиска Фибоначчи для N-2. При исходном интервале (О, f j] (f 2=2) значения f надо подсчитать в двух точках, отвечающих Fa н fi, а точнее в Xi=\ и х:2=1+6, где 6 «пренебрежимо мало». При этом независимо от соотношения между значениями f{x и f{x новый интервал неопределенности будет иметь длину, «почти равную» половине начальной (см. левую диаграмму на рнс. 41). На рис. 4f изображена также ситуация с тремя вычислениями функции. В этом примере длина начального интервала неопределенности равна [О, Fs\ (FaS) и в качестве двух первых внутренних точек берутся Fi и F (т. е, л:,=1, x=2). В соответствии с соотношением между значениями /(л:,) и f(x новым интервалом неопределенности будет [О, 2]. В середине его значение f уже известно. Поэтому, чтобы получить окончательный интервал длины (1--6), требуется только одно дополнительное вычисление функции. Результатом поиска Фибоначчи с N вычислениями функции является интервал неопределенности, составляющий (с точностью до Б) МРц-ю часть длины исходного интервала, 4.1.2,2, Метод золотого сечения. Поиск Фибоначчи удобен далеко не всегда, В частностк, он плохо подходит для решения одномерных подзадач, возникающих в схемах многомерной минимизации. Запросы к точности решений таких подзадач практически нн-никогда не формулируются в терминах числа обращений к процедуре расчета функции. Значит, для них пришлось бы либо хранить избыточный набор чисел Фибоначчи, либо многократно генерировать эти числа по мере необходимости. К тому же поиск Фибоначчи нелегко приспособить к часто используемому критерию остановки, требующему, чтобы значения функции на окончательном интервале неопределенности разнились не более чем на заданную величину. Из-за указанных недостатков поиска Фибоначчи вместо иего часто используют другую, почти столь же эффективную теоретически, lira где т есть решение квадратного уравнения т=--т-1 =0. На этом числе и основан рассматриваемый метод. Когда он применяется к начальному интервалу [О, I], первыми пробными внутренними точками будут т н 1-т (т. е. примерно 0.6180 и 0.3820). Затем левый или правый кусок интервала будет отброшен, но в том и другом случае одна из этт1х точек обязательно окажется внутренней для нового интервала, делящей его две части, длины которых снова относятся. О 1-г г 1 Рис 4g. Расположение точек в методе золотого сечения. как т к 1-т. Золотое сечение можно, таким образом, рассматривать как предельный случай поиска Фибоначчи, Расположение точек в этом методе показано иа рнс. 4g. В процедуре золотого сечения длина интервала неопределенности на каждом шаге уменьшается в т раз, т. е. сходится к нулю линейно. 4.1.2.3. Полиномиальная интерполяция. В методах золотого сечения н поиска Фибоначчи выбор очередного интервала неопределенности всегда ограничен только двумя альтернативами. При этом в правиле, на основании которого осуществляется этот выбор, учитываются лишь соотношения между значениями функции /, ио не сами значения, Еслн же / - гладкая функция, используй ее значения, можно, как н в случае с поиском нуля, получать существенно более быстродействующие процедуры минимизации. Общий принцип их функционирования таков: на каждом шаге f аппроксимируется некоторой модельной функцией J, точку минимума которой найти легко, и эта точка берется в качестве текущего приближения искомой. Поскольку линейная функция (если она не постоянна) конечного минимума не имеет, простейшей пригодной моделью функции f будет парабола вида f=lfix+bx \-с. Если й>0, то / имеет минимум в точке х*, удовлетворяющей равенству ах*+Ь=Ь. ритма. Он запускается в точке (-1.2, 1.0). Видно, что для перехода в окрестность решения потребовалось довольно много вычислений функции. Хотя метод многогранника не предназначен для гладких задач, все же пример достаточно показателен. Надо только добавить, что в общем случае с негладкой функцией он будет работать несравненно хуже, чем в рассмотренном. 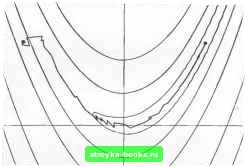 Рис. 41. Траектория поиска минимума функции Розенброка методом многогранника. *4.2.3. СОСТАВНЫЕ НЕДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ На практике нередко возникают задачи минимизации функций, которые сами по себе являются негладкими, но составлены нз гладких. В таких случаях один из подходов к поиску решения может заключаться в том, чтобы заменить негладкую составную задачу безусловной минимизации эквивалентной ей гладкой задачей с ограничениями. Затем можно попытаться решить последнюю каким-нибудь методом оптимизации прн ограничениях, учитывающим ее специфику. Соответствующие методы рассмотрены в разд. 6.8. Следует подчеркнуть, что в библиотечных программах решения неглад-кит задач, о которых идет речь, указанное преобразование, как правило, реализуется неявно, так что пользователь может и не догадываться о нем. Типы применяемых преобразований проиллюстрированы ниже иа примере трех наиболее часто встречающихся составных задач. Пример 4.3, Первой рассмотрим задачу вида найти min max {fi(x), [(х).....f„(x)}. (4.3) где {fi (x)} - набор гладких функций. Эта негладкая задача преобразуется в гладкую введением новой переменной x„+i, имеющей при данном х смысл верхней границы для всех значений {/((х)}. Получающаяся в результате эквивалентная (4.3) задача формулируется так: найти min x„+i при ограничениях fi{x)x„ i=l, .. В ней есть п нелинейных ограничений-неравенств, т. е. она принадлежит классу задач, значительно более сложных по структуре, чем задачи безусловной минимизации. Таким образом, гладкость достигнута ценой усложнения структуры, и это принципиальный момент. Пример 4.4. Следующей возьмем задачу /j! найти min S f, (х) . (4.4) В ее названии отражено, что минимизируемой функцией является р-норма вектора (/,(х), г(х), ..., f„,(x)) с р=1 (см. разд. 2.2.4.2). Построение гладкого аналога задачи (4.4) опирается на тот простой факт, что значение Д (х) всегда можно расщепить на положительную и отрицательную составляющие. Точнее говоря, всегда возможно представление ft(x)=ri-s,., где величины и s, неотрицательны. Прн этом гарантировано неравенство )/i (х) /•(-!--s, обращающееся в равенство, когда Si/-; =0. Отсюда ясно, что задача (4.4) эквивалентна следующей: найтн min 2 (ri-fSi) jfeffl"; s.re&."= при ограничениях , (х) = /-,-s,., ( = 1, 2, .. г,.>0; s,>0, i=l, 2, .. Пример 4.5. В заключение рассмотрим задачу иайти min 2 max), (х), 0}. 5 № S9B4 ., т; , т. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [ 19 ] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] 0.0016 |