
 |
|
Главная Методы условной оптимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [ 24 ] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] вычислять Gj по формуле Ясно, что существенно положительно определенная матрица Gj останется неизменной. Расчет факторов знаконеопределенного симметричного разложения можно организовать так, что он потребует около п арифметических операций и 0{п) операций сравнения. Схожая факторизация, требующая 0{п) сравнений, предложена Флетчером (1976), а также Банчем и Кауфманом (1977). Модифицированный метод Ньютона можно строить на базе любой численно устойчивой процедуры факторизации знаконеопределенной CHNaieTpH4H0fi матрицы. Мы рассмотрели три из них. Другие читатель найдет, например, у Осена (1971), Кэииела и Дэкса (1979). Когда матрица Сд не является знакоопредсленной и соответственно существуют иаправ.пения отрицательной кривизны, учитывать их при выборе ри можно по-разному. Ранее была сформулирована одна из простейших стратегий; брать в качестве р решение уравнения (4.18) во всех случаях, когда норма градиента достаточно велика по отношению к модулю значения целевой функции, а иначе - использовать в роли /з какое-нибудь из направлений отрицательной кривизны. При этом направления отрицательной кривизны будут вычисляться только вблизи седловой точки. Сформулированное правило можно расценивать как конкретную реализацию более общего правила, заключающегося в том, чтобы определять по формуле PhWi+fiPi, где pi- решение уравнения (4,18), рг- направление отрицательной кривизны, а и фг- неотрицательные числа. Подразумевается, что в случае положительной определенности матрицы Gs вес фа равен нулю, а (р,- единице (тем самым из формулы убирается несуществующий вектор рг). Если в упомянутой выше стратегии нулевой вес ф1 является исключением, то Флетчер и Фриман (1977), например, считают, что брать ipi ну.певым надо как можно чаще, Грэхем (1976) предлагает определять веса по норме поправки для матрицы Гессе Gj, при переходе от Gj, к G, Более общие схемы, Б которых ф, и фа вычислякл-ся как функции длины шага а, можно иайти в работах Мак-Кормика (1977), Море и Соренсена (1979) и Гольдфарба (1980), В замечаниях к разд. 4.3 было отмечено, что методы безусловной минимизации гладких функций распадаются иа два обширных класса. Имеются в виду «методы с регулировкой шата» и «методы доверительной окрестности». Хотя в данной книге основное внимание уделяется первым, приш.па пора поподробнее поговорить и о вторых. Исходной посылкой для построения методов довершельной окрестности служит суждение о том, что на точку минимума модельной квадратичной функции разумно ориентироваться лишь при усло- ВИИ, что она ищется в области, где эта функция хорошо описывает поведение F. Размеры такой области предлагается характеризовать ограничением на величину нормы вычисляемого вектора направления поиска. Формализованное правило выбора очередной точки jc+j, воплощающее высказанные идеи, звучит так: в качестве х,+, надо брать сумму x-bPt, где р-решение при некотором Д вспомогательной задачи вида (4.24) найти mm(glp-[-~pGtp) при ограничении pj:u. Как искать такие p;i, подсказывает следующее соображение: если Х- число, при котором матрица G+ll положительно определена, то решение р системы уравнений (Cft-I-H)p -вб (4.25) будет решением задачи (4.24) с А ЦрЦг, когда Х=0, и с Д=(1ра, когда X > 0. Соответственно р можно вычислять как решение (4.25). Из сказанного ясно, что при положительно определенной матрице G и достаточно большом Д решение задачи (4.24) будет обычным ньютоновским направлением (т. е. решением системы (4.25)) с Х = 0, а если при каком-то Д оно окажется отличным от ньютоновского направления, то это является признаком существенности ограничения на норму вектора р и будет означать, что рг = А. В методе доверительной окрестности направление поиска обычно определяется просмотром решений задачи (4.24) при нескольких значениях параметра Д. В результате выбирается вектор р, для которого величина F {х + р) «существенно меньше», чем Р{х). Такой вектор всегда найдется, так как при достаточно малом А квадратичная аппроксимация хорошо описывает поведение F. Нетрудно показать, что при АО вектор р, убывая по норме до нуля, стремится по направлению к антиградиенту. Идея построения правила расчета направления поиска на основе понятия доверительной окрестности принадлежит Левенбергу (1944) и Маркардту (1963). Они сформулировали ее для задач о наименьших квадратах (см. разд. 4.7.3). Применение данного подхода к функциям общего вида обсуждалось Гольдфельдом, Квандтом и Трот-тером (1966). В некоторых методах доверительной окрестности k-я итерация начинается с решения уравнения (4,25) при Х = 0. Если по ходу вычислений выясняется, что матрица не является знакоопредсленной или норма 1р найденного решения оказывается больше текущего порогового значения д, то вк.пючается процедура поиска приближенного решения нелинейного уравнения вида Ч(?)=11(С-ЬХ/)-в,а = Д. (4.26) Квадрат функции, стоящий в его левой части, можно представить п / т \а Здесь (Ui), {Х;} - собственные векторы и числа матрицы Gj. Таким образом, ff"!}) является рациональной функцией с полюсами в точках X, совпадающих с собственньми значениями матрицы -Сд. Хебден (1973) предложил применять для поиска корня уравнения (4.26) регуляризованный метод с рациональной интерполяцией (см. разд. 4.1.1.4). Его процедура не требует построения спектрального разложения Од и использует при вычислении значений tf(X) и dtfldl. разложение Холесского для матрицы Gj+W. Если при каком-то к расчет факторов этого разложения выявляет знаконеоп-ределенность Gjl XI, то находится число р, такое, что 0+U+\l будет положительно определенной матрицей, и в качестве очередной оценки решения (4.26) берется сумма X-fp. Поиск приближенного корня уравнения (4.26) методом Хебдена обычно требует двух- или трехкратного построения разложения Холесского. Когда матрица Gh не является знякоопределенной, независимо от установленной точности вычисления X понадобится не менее двух разложений. После того как удовлетворительное решение уравнения (4.26) и соответствующий вектор р найдены, выполняется проверка пригодности точки лтд! р на роль очередного приближения х;,.,. Она подойдет, если значение f (x-fp) окажется существенно меньшим, чем fj (эталоном служит изменение, предсказываемое по квадратичной аппроксимации). В противном случай найденный вектор р отбрасывается, порог Д уменьшается (например, Д можно пересчитывать на основе кубической интерполяции с использованием значений функции F и ее производных в точках л:д н х,,+р) и снова вызывается процедура решения уравнения (4.26). Когда уменьшение F признано прием.пемым, можно попытаться увеличить Д. Детали различных схем пересчета Д читатель найдет в работах Флегчерэ (1971а, 1980), Гэя (1979а), Хебдена (1973), Море (1977) и Соренсена (1980а). Подробное обсуждение процедуры расчета р при фиксированном Д приведено в работе Гэя (1979b). Важно отметить, что у методов с регулировкой шага и у методов доверительной окрестности есть много общих черт. (1) И те и другие конструируются так, чтобы при приближении к точке мин My.ia хорошей функции онн становились эквивалентными к.пассическому методу Ньютона. (2) И в тех и в других очередное приближение определяется некоторой скалярной величиной, значение которой подбирается из условия согласования истинного изменения функции F и его оценки, получа.ощеися по квадратичной модели. В методах с регулировкой шага этим скаляром является длина шага «д, а в методах доверительной окрестности- порог Д. Правда, принципы выбора и Д различны. Ве- личина Яд ищется как приближение «идеа.чьного» шага (шага в точку минимума вдоль направления рд), а Д подбирается в соответствии с «качеством» предыдущих значений F без ориентации на какой-то «идеал». (3) Если матрица Gj не является знакоопределенной и норма §д мала или равна нулю, методы обоих типов должны сделать шаг вдоль направления отрицательной кривизны, вычисляемого по разложению самой Gf или ее модифицированной версии. (4) Когда матрица Од становится зиако-неопреде.ленной при «большом» градиенте (что существенно усложняет .задачу предварите.пьной оценки нормы лд+,-лгдЦ). в методах обоих типов расчет л:д+, ориентируется на ее положительно определенную «составляющую». В методах с регулировкой шага это проявляется явно, в соответствующей модификации Од, а в методах доверительной окрестности-неявно, через связь -Ч1 с размерами предыдущих шагов, выполненных при положительно определенных Од. Хорошая реализация метода доверительной окрестности всегда включает какие-то элементы, присущие методу с регулировкой шага, и наоборот. Например, в алгоритме с регулировкой шага обязательно должно быть предусмотрено шраничение на длину шага вида llxj+i-Лд<Д (см. разд. 4.3.2.1). В свою очередь хороший метод доверительной окрестности будет использовать для настройки Д какую-нибудь регуляризованную процедуру с полиномиальной интерполяцией. Сходство между методами обоих типов наиболее отчетливо проявляется в следующей ситуации. Предположим, что они запускаются в точке Хд, где матрица Од положительно определена. Пусть далее ньютоновское направление р в Лд таково, что р<Д и f (Хд-(-р) > fj. Тогда алгоритм с регулировкой шага будет искать с помощью полиномиальной интерполяции длину шага а (с( < 1) вдоль р, обеспечивающую существенное убьЕвание функции F. Аналогичная величина а будет вычислена и в методе доверительной окрестности, только здесь оиа сыграет роль множителя при пересчете порога Д. После этого пути алгоритмов разойдутся. В методе с регулировкой шага очередным приближением станет точка Хд-f ар, лежащая в прежнем направлении, а в методе доверительной окрестности шаг будет сделан в ново.ч направлении, найденном из решения нелинейного уравнения (4.26) с меньшим значением Д. Наряду со сходными чертами между методами с регулировкой шага и методами доверительной окрестности имеются н значительные различия. Наиболее важные связаны с характером использования информации о вторых производ!Ш1х. В методах с регулировкой шага матрицу Од стараются модифицировать так, чтобы изменения не затрагивали подпространства, натянутого на ее собственные векторы с положительными собственными значениями. Это гарантирует сохранность существенно положительно определенных Од. Если же замена Gj осуществляется в методе доверительной окрестности, то она отражается на всех векторах, так как результатом замены G на Gft+X/ будет сдвиг иа ?. всех собственных значений. При этом замены возможны независимо от определенности С, т. е., даже если Gj существенно положительно определена, направление поиска в методе доверительной окрестности может отличаться от ньютоновского. В подзадаче (4.24) ограничение на длину вектора р ставится через евклидову норму. Выбор именно этой нормы объясняется относительной простотой поиска приближенного решения (4.24). Если же посчитать целесообразным тратить на определение пробных р больше усилий, то люжио пользоваться и другими нормами. Флетчер (1972а), например, предлагал подчинять выбор р простым ограничениям вида В этом случае для построения р надо решить задачу поиска минимума квадратичной формы на параллелепипеде. 4.5. МЕТОДЫ ПЕРВОГО ПОРЯДКА 4.5.1. НЬЮТОНОВСКИЕ МЕТОДЫ С КОНЕЧНаР.АЗНОСТНОЙ АППРОКСИМАЦИЕЙ Для ТОГО чтобы получить быстросходящийся алгоритм безусловной минимизации, не обязательно пользоваться точными значениями вторых производных. Метод, практически ие уступающий в скорости сходимости методу Ньютона, можно построить на основе аппроксимации матрицы Гессе по конечным разностям градиентов. Во многих случаях такой метод окажется самым подходящим. Имеются в виду ситуации, когда вычисление аналитических значений вторых производных минимизируеьюй функции F затруднено или просто невозможно. За оценку /-го столбца матрицы Gf обычно принимают его правую конечно-разностную аппроксимацию f/, = i-((*+te,)-gW). Здесь h-число, именуемое конечпо-разностпьш интервалом, а е, есть i-й единичный вектор, выполняющий функцию конечно-разностного направления. В данном разделе мы ради простоты изложения будем полагать, что все конечные разности вычисляются на одном и том же интервале h. На самом же деле приходится строить набор интервалов {Л;}, ! = 1.....и, и технически делается это так, как описано в разд. 8.6. Матрица К, составленная из столбцов у,, вообще говоря, несимметрична. Поэтому для аппроксимации матрицы Гессе G, берут полусумму Gt = /2(K-f Кг), которая симметрична по построению. Метод, получающийся из обычного ньютоновского заменой в уравнении (4.17) матрицы на б, будем называть дискретным методом Ньютона. Подобно своем.у классическому прототипу, он порождает целый класс модифицированных методов; понятно, что техника модификаций, разработанная для обоб!деиия метода Ньютона на случаи с знаконеопределенными Gfi, применима и к его конечно-разностному аналогу. Коль скоро предполагается использовать коиечно-разностную аппроксимацию, то естественно встает вопрос о выборе величины интервала Л. Здесь обнаруживаются определенные противоречия между теорией и практикой оптимизации. Если бы расчеты на машинах проводились с абсолютной точностью, для достижения квадратичной сходимости дискретного метода Ньютона надо было бы по мере убывания g устремлять h к нулю. В действительности же очень малые величины h недопустимы, так как при таких h вычисляемые значения элементов матрицы нз-за больших ошибок компенсации (см. разд. 2.1.5) не будут иметь никакого смысла. Значит, интервал h, с одной стороны, должен быть достаточно мал, чтобы обеспечивать удовлетворительную сходимость, а с другой - достаточно велик, чтобы гарантировать приемлемую точность вычисления конечно-разностной аппроксимации. Нужен компромисс, и, к счастью, найти его не так уж трудно. Дело в том, что для большинства практических задач эффективность метола не очень чуастви- 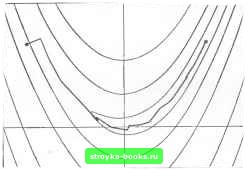 Рис. 41. Траектория поиска минимума функции Розенброка дискретным методом Ньютона, тельна по отношению к выбору h (чего нельзя сказать о выборе интервала конечно-разностной аппроксимации градиента в методах без вычисления производных, рассматриваемых в разд, 4.6), Подробнее вопрос о назначении h будет разбираться в разд, 8.6. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [ 24 ] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] 0.0012 |